Таким образом, размышляя над тем, следует ли вам принимать предложение другого игрока, будьте уверены в том, что, если отклоните его предложение сегодня и предложите, в свою очередь, δ(1 – L) завтра, он согласится. Если вы знаете, что у вас есть возможность заставить другого игрока принять предложение δ(1 – L) завтра, это значит, что завтра вам наверняка достанется доля 1 – δ(1 – L).

Следовательно, сегодня вы не должны принимать предложение меньшее, чем δ(1 – δ(1 – L)). Это дает нам следующее минимальное значение L:

L ≥ δ(1 – δ(1 – L))

или

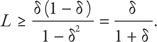
Вы не должны принимать ничего меньше δ / (1 + δ), поскольку можете получить больше, если подождете и сделаете контрпредложение, на которое другая сторона обязательно согласится. По этой же логике другой игрок также не примет ничего меньше δ / (1 + δ). Это позволяет определить величину максимального предложения, на которое вы можете рассчитывать.

Обозначив буквой М максимальную долю, на которую вы можете рассчитывать, определим, при каком значении М вы не станете отклонять предложение. Поскольку вам известно, что другой игрок не примет ничего меньше δ / (1 + δ) в следующем раунде, вы можете получить максимум 1 – δ / (1 + δ) = 1 / (1 + δ) в следующем раунде. Если это лучшее, что вы можете сделать в следующем раунде, то сегодня вам следует принять предложение δ(1 / (1 + δ)) = δ / (1 + δ).

Таким образом, мы имеем:

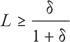
и

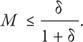
Это означает, что минимальное предложение, которое вы можете когда-либо принять, составляет δ / (1 + δ) и что вы всегда должны принимать любое предложение, равное или превышающее δ / (1 + δ). Поскольку эти два значения эквивалентны, именно это вы и получите. Другой игрок не предложит вам меньше, поскольку вы отклоните такое предложение. Он не предложит вам и больше, поскольку вы наверняка примете предложение δ / (1 + δ).

Такой способ раздела «пирога» имеет смысл. Есть все основания предположить, что по мере сокращения промежутка времени между предложением и контрпредложением участники торга становятся более нетерпеливыми, или, говоря языком математики, значение переменной δ приближается к 1. Проанализируем крайний случай, когда δ = 1. Предложенный принцип дележа будет таким:

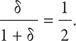
Таким образом, в данном случае «пирог» будет разделен между двумя сторонами поровну. Если ожидание своей очереди ничего не стоит, тогда игрок, делающий предложение первым, не имеет никаких преимуществ, поэтому самое разумное – разделить «пирог» по принципу 50:50.

Теперь представьте себе другую крайность: «пирог» вообще исчезнет, если предложение не будет принято. Это уже игра в ультиматум. Если стоимость договоренности, достигнутой завтра, равна нулю, тогда δ = 0, а принцип дележа (0, 1) – точно такой же, как и в ультимативной игре (со всеми ее оговорками).

Для того чтобы проанализировать промежуточный вариант, представьте себе, что время имеет значение и что каждый случай промедления приводит к потере половины «пирога», или δ = ½. Теперь принцип дележа будет таким:

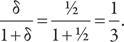
Поясним это следующим образом. Человек, делающий вам предложение, претендует на весь «пирог», которого просто не будет, если вы скажете «нет». Это дает ему ½ «пирога» сразу же. Из оставшейся половины «пирога» вы можете получить половину, или ¼ целого «пирога», и эта доля будет утрачена, если другой игрок не примет ваше предложение. Теперь, после двух раундов игры, другой игрок получит ½, а вы – ¼ «пирога», а это значит, что мы вернулись к тому, с чего начинали. Таким образом, в любой паре предложений другой игрок может получить в два раза больше, чем вы, что приводит к разделению «пирога» в соотношении 2:1.

В нашем варианте решения оба участника игры в равной степени терпеливы. Этот метод можно использовать и в том случае, когда у двух игроков разная стоимость ожидания. Логично предположить, что более терпеливый игрок получит большую долю «пирога». На самом деле при сокращении промежутка времени между двумя предложениями «пирог» делится в соотношении, отображающем стоимость ожидания для двух игроков. Следовательно, если один игрок в два раза более нетерпелив по сравнению с другим, он получит одну треть «пирога», или половину того, что получит другой игрок {154}.

Тот факт, что большая доля во время переговоров достается более терпеливой стороне, неблагоприятен для Соединенных Штатов. Американская система правления и ее освещение в средствах массовой информации культивируют нетерпеливость. Когда переговоры с другими странами по военным или экономическим вопросам продвигаются медленно, отслеживающие свой интерес лоббисты ищут поддержки у конгрессменов, сенаторов и СМИ, которые оказывают на администрацию давление в целях ускорения процесса и получения результатов. Страны, с которыми США ведут переговоры, прекрасно знают об этом, благодаря чему могут добиться более весомых уступок.

Глава 12
Голосование

Я не дам себе труда уважать

Того, кто не дает себе труда голосовать.

Огден Нэш

УВАЖЕНИЕ К ВОЛЕ НАРОДА, выраженной посредством голосования, – это основа демократического государства. К сожалению, реализовать эти высокие идеалы на практике не так уж просто. В процессе голосования, как и в любой игре с участием многих игроков, возникают вопросы, решение которых требует стратегического подхода. Под влиянием тех или иных причин избиратели часто искажают свои истинные предпочтения. Ни принцип большинства, ни любая иная схема голосования не способны решить эту проблему, поскольку идеальной системы, которая позволяла бы объединить индивидуальные предпочтения в волю всего народа, просто не существует [144] .