Запишите где-нибудь ответ на этот вопрос и продолжайте читать. Для того чтобы понять, как следует играть в эту игру, и сопоставить правильную стратегию с тем, как на деле сыграли оба племени, обратите внимание на два показательных момента. Во-первых, перед началом игры оба племени получили по несколько минут на обсуждение этого испытания. Один из членов племени Чуай Ган, афроамериканец Тед Роджерс, который был разработчиком программного обеспечения, отметил: «В конце игры мы должны оставить их с четырьмя флажками». Это действительно так: оставшись с 4 флажками, племя Сук Джай должно убрать 1, 2 или 3 флажка. В таком случае племени Чуай Ган останется только дождаться своей очереди, убрать 3, 2 или 1 флажок соответственно – и победить. В племени Чуай Ган правильно поняли и использовали эту возможность: когда оставалось 6 флажков, они убрали два из них.

Но есть еще один показательный момент. На предыдущем ходе, когда племя Сук Джай забрало 3 флажка из оставшихся 9, одна из представительниц этого племени Ши Энн, которая умела четко формулировать мысли и по праву гордилась своими аналитическими способностями, вдруг осознала: «Если Чуай Ган возьмет два флажка, нам конец». Это означало, что племя Сук Джай только что сделало неправильный ход. Что же следовало делать дальше в этой ситуации?

Ши Энн или одному из ее соплеменников следовало бы размышлять так же, как это сделал Тед Роджерс, и попытаться оставить другое племя с четырьмя флажками, но применив эту логику к следующему ходу этого племени. Как оставить другое племя с 4 флажками на его следующем ходе? Оставив его с 8 флажками на предыдущем! Когда это племя заберет 1, 2 или 3 флажка из восьми, вы возьмете 3, 2 или 1 флажок, оставив его с четырьмя флажками, как и планировали. Следовательно, племени Сук Джай необходимо было бы поменяться местами с племенем Чуай Ган и взять только 1 флажок из 9. Аналитический ум Ши Энн начал активно работать, но с опозданием на один ход! По всей видимости, у Теда Роджерса аналитические способности были еще лучше. Но так ли это?

Почему племя Сук Джай оказалось с 9 флажками на предыдущем ходе? Потому что в Чуай Ган убрали с поля 2 флажка из 11 на своем предыдущем ходе. Теду Роджерсу следовало продолжить свои рассуждения на один ход дальше. Племени Чуай Ган нужно было забрать 3 флажка, оставив Сук Джай с 8 флажками – а это проигрышная позиция.

Эти же рассуждения можно продолжить в обратном порядке. Для того чтобы оставить другое племя с 8 флажками, вам следует оставить его с 12 флажками на предыдущем ходе; для этого необходимо оставить его с 16 флажками на ход раньше и с 20 флажками на ход до этого хода. Таким образом, племени Сук Джай следовало начать игру, убрав с игрового поля только 1 флажок, а не 2, как случилось на самом деле. Такой ход обеспечил бы этому племени неизбежную победу, оставив племя Чуай Ган с 20, 16, … 4 флажками на очередных ходах {35}.

А теперь вспомним первый ход племени Чуай Ган. У них было 19 флажков. Если бы в Чуай Ган придерживались своей же логики, им следовало взять 3 флажка, оставив Сук Джай с 16 флажками и тем самым обрекая это племя на неизбежное поражение. Начиная с любого этапа игры, на котором соперник произвел неправильный ход, команда, делавшая очередной ход, могла перехватить инициативу и выиграть. Но племя Чуай Ган тоже играло не идеально {36}.

В таблице показаны как фактические, так и правильные ходы обоих племен на каждом этапе игры. (Запись «Нет хода» означает, что любой ход проигрышный при условии, что соперник делает правильный ход.) Из этой таблицы видно, что практически во всех случаях оба племени делали неправильный выбор. Исключением стал только ход племени Чуай Ган, когда они оказались с 14 флажками, но даже он, скорее всего, был случайным, поскольку на следующем ходе племя убрало с поля 2 флажка из 11, тогда как следовало взять 3 флажка.

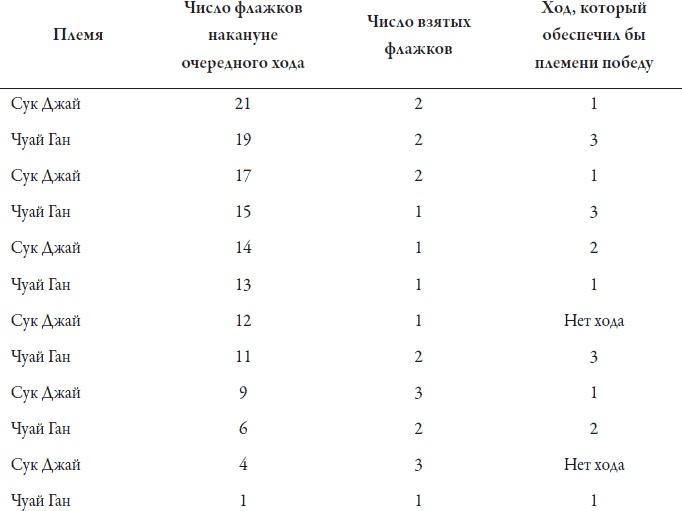
Не судите эти племена слишком строго: для того чтобы научиться играть даже в самые простые игры, требуются время и опыт. На своих занятиях мы проводили эту игру парами или в группах студентов и пришли к выводу, что даже студентам первого курса университетов Лиги плюща {37} требуется сыграть три или даже четыре раунда, прежде чем они полностью усвоят логику игры и начнут играть правильно с первого хода. (Кстати, какое число флажков выбрали вы, когда мы попросили вас сделать это, и как аргументировали этот выбор?) Следует отметить, что люди обучаются быстрее, когда наблюдают за игрой со стороны, чем когда играют сами. Возможно, позиция наблюдателя позволяет увидеть общую картину игры и строить свои рассуждения более спокойно, чем в роли участника.

Для того чтобы помочь вам лучше понять логику рассуждений в этой игре, предлагаем первую задачу для тренировки мышления (такие задачи помогут вам отработать навыки стратегического мышления). Ответы вы сможете найти в конце книги, в разделе «Решения».

ЗАДАЧА ДЛЯ ТРЕНИРОВКИ МЫШЛЕНИЯ № 1

Позвольте нам изменить правила игры на прямо противоположные: теперь вы выиграете, если заставите другую команду взять последний флажок. Сейчас ваш ход, и у вас 21 флажок. Сколько флажков вы возьмете?

Теперь, когда вы укрепили свое мышление, решив эту задачу, рассмотрим другие элементы стратегии, которая применяется в играх данного класса.

Почему метод обратных рассуждений делает игры разрешимыми

У игры с флажками было одно свойство, которое делало ее полностью разрешимой, – это отсутствие неопределенности любого вида, будь она обусловлена естественным элементом случайности, мотивами и возможностями других игроков или их фактическими действиями. На первый взгляд, это довольно простая идея, и все-таки она требует уточнения и разъяснения.

Во-первых, на любом этапе игры, когда племя должно было сделать свой ход, ему были известны все условия игры, в частности, сколько осталось флажков. Во многих других играх присутствует элемент чистой случайности, которую создает сама природа или боги случайностей. Например, во многих карточных играх дело обстоит так: когда игрок принимает решение, он не знает наверняка, какие карты на руках у других игроков, хотя может делать какие-то предположения на основании их предыдущих действий. В следующих главах рассматриваются игры, в которых присутствует естественный элемент случайности.