В заключение следует отметить, что игра в труса иллюстрирует один общий аспект игр: хотя в описанных играх позиции обоих игроков идеально симметричны с точки зрения их стратегий и выигрышей, равновесие Нэша в игре может быть ассиметричным, то есть игроки могут выбрать разные стратегии.

Немного истории

В этой и предыдущей главах мы привели несколько примеров игр, которые стали классическими. Безусловно, о дилемме заключенных знают все. Однако игра с двумя охотниками из каменного века, которые пытаются встретиться для совместной охоты, почти так же известна. Жан-Жак Руссо описал практически идентичный сценарий этой игры, хотя у него, конечно же, не было Флинтстоунов {72}, чтобы сделать этот сценарий более красочным.

Игра со встречей охотников отличается от дилеммы заключенных, поскольку лучший ответный ход Фреда состоит в том, чтобы сделать то же, что сделает Барни (и наоборот), тогда как в игре с дилеммой заключенных и у Фреда, и у Барни была бы своя доминирующая стратегия: только один вариант возможных действий (скажем, охота на кролика) был бы оптимальным для каждого игрока независимо от того, что сделает другой. Между этими играми есть еще одно различие: в игре со встречей охотников Фред выбрал бы охоту на оленя, если бы мог убедиться (посредством прямого общения или благодаря существованию фокальной точки) в том, что Барни тоже выберет охоту на оленя, и наоборот. По этой причине данную игру часто называют игрой на доверие.

Руссо описывал эту идею не на языке теории игр, и его формулировка оставляет смысл игры открытым для разных интерпретаций. В интерпретации Мориса Крэнстона в качестве крупного зверя выступает олень, а формулировка самой задачи выглядит так: «Если охотились на оленя, то каждый понимал, что для этого он обязан оставаться на своем посту; но если вблизи кого-либо из охотников пробегал заяц, то не приходилось сомневаться, что этот охотник без зазрения совести пустится за ним вдогонку и, настигнув свою добычу, не станет сокрушаться о том, что лишил добычи своих товарищей» [54] . Разумеется, если другие охотники отправились в погоню за зайцем, больше ни одному охотнику не было смысла преследовать оленя. Тем не менее в более распространенной интерпретации это игра на доверие, в которой каждый охотник предпочитает присоединиться к охоте на оленя, если все остальные поступят так же.

В той версии игры в труса, которая стала знаменитой благодаря фильму Rebel Without a Cause («Бунтарь без идеала»), два парня едут на своих автомобилях параллельно друг другу по направлению к крутому обрыву; трусом станет тот, кто первым выпрыгнет из машины. Бертран Рассел и другие ученые использовали эту игру в качестве метафоры ядерной конфронтации. Томас Шеллинг подробно описал ее в своей новаторской работе по теории игр, посвященной анализу стратегических ходов; мы вернемся к этой теме в главе 6.

Насколько нам известно, игра «семейный спор» не имеет таких корней в философии или массовой культуре. О ней идет речь в книге Данкана Люче и Говарда Райффа Games and Decisions («Игры и решения») – первой классической книге по формальной теории игр [55] .

Поиск равновесия Нэша

Как найти равновесие Нэша? Худший из всех возможных способов – анализ каждой ячейки таблицы выигрышей. Если в одной из ячеек оба выигрыша представляют собой оптимальный ответный ход, значит стратегии и выигрыши, соответствующие этой ячейке, образуют равновесие Нэша. Если таблица большая, эта процедура может стать весьма утомительной. Но Бог создал компьютеры именно для того, чтобы спасти людей от столь утомительного анализа и громоздких вычислений. Существует несколько пакетов прикладных программ для поиска равновесия Нэша [56] .

Однако в некоторых случаях есть и более короткие пути решения этой задачи; приведем описание одного из них.

Метод последовательного исключения

Вернемся к ценовой игре между компаниями Rainbow’s End и B. B. Lean. Вот таблица выигрышей для этой игры.

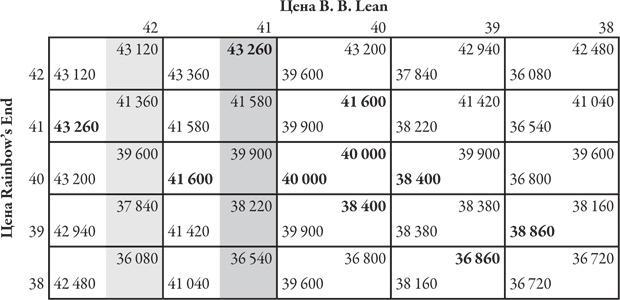
RE не знает, какую цену выберет BB. Но RE может определить, какую цену или цены BB не выберет: BB никогда не установит на свой товар цену 42 или 38 долларов. Тому есть две причины (в нашем примере присутствуют обе, но в других ситуациях может быть задействована только одна из причин) [57] .

Во-первых, каждая из этих стратегий однозначно хуже для BB, чем любая другая доступная стратегия. Независимо от того, какую стратегию собирается выбрать RE, для BB 41 доллар – это лучше, чем 42, а 39 долларов лучше, чем 38. Для того чтобы понять это, сравните выигрыши в случае выбора стратегии «41 доллар» и стратегии «42 доллара»; то же касается и другой пары стратегий. Сравните пять чисел, соответствующих прибыли BB в случае выбора цены 41 доллар (они выделены темно-серым цветом), с показателями прибыли, полученной в случае выбора цены 42 доллара (они выделены светло-серым цветом).

В каждом из пяти вариантов выбора RE прибыль BB в случае выбора цены 42 доллара будет меньше, чем в случае выбора цены 41 доллар:

43 120 < 43 260 41 360 < 41 580 39 600 < 39 900 37 840 < 38 220 36 080 < 36 540

Следовательно, какими бы ни были ожидания BB в отношении действий RE, BB ни при каких условиях не выберет цену 42 доллара, поэтому RE может смело рассчитывать на то, что BB исключит из рассмотрения стратегию выбора цены 42 и 38 долларов.

Когда одна стратегия (предположим, стратегия А) однозначно хуже для одного из игроков, чем другая (скажем, стратегия Б), говорят, что стратегия А доминируемая по отношению к стратегии Б. Если такая ситуация действительно наблюдается, этот игрок ни при каких обстоятельствах не применит стратегию А, хотя использует ли он стратегию Б, остается только гадать. В таком случае другой игрок может с уверенностью строить свои рассуждения, опираясь на эту информацию; в частности, ему нет необходимости анализировать стратегию, которая была бы оптимальным ответным ходом только на стратегию А. Следовательно, в процессе поиска решения этой игры можно полностью исключить доминируемые стратегии из рассмотрения. Это позволяет сократить размер таблицы игры и упростить ее анализ {73}.