Book.

Таблицы выигрышей для таких игр можно упростить, указывая в них выигрыш одного игрока, поскольку выигрыш другого можно рассматривать как величину, равную разнице между постоянной суммой (в нашем примере 100) и выигрышем первого игрока. Как правило, в явной форме указывается выигрыш игрока, которому соответствуют строки таблицы. В данном примере для такого игрока предпочтителен результат с более высокими показателями, а для игрока, которому соответствуют столбцы таблицы, оптимален результат с более высокими показателями. С учетом этих правил таблица выигрышей для штрафного броска выглядит так:

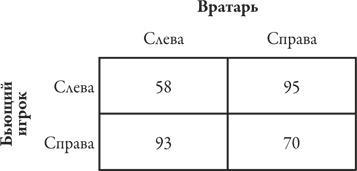
Если вы игрок, выполняющий штрафной удар, какой из двух стратегий отдали бы предпочтение? Если вы выберете стратегию «справа», вратарь может удержать ваш процент забитых мячей на уровне не выше 58, выбрав стратегию «слева»; если же вы выберете стратегию «справа», вратарь может удержать ваш процент забитых мячей на уровне не выше 70, тоже выбрав стратегию «справа» {78}. Из этих двух вариантов вам лучше выбрать сочетание «справа», «справа».

Можете ли вы получить лучшие результаты? Предположим, вы выбираете стратегию «слева» или «справа» случайным образом в пропорции 50:50. Например, когда вы уже готовы подбежать к мячу и нанести по нему удар, подбросьте монетку, которую держите в руке так, чтобы этого не видел вратарь, и выберите «слева», если выпадет решка, и «справа», если выпадет орел. Если вратарь выберет стратегию «слева», ваша смешанная стратегия обеспечит вам попадание в ½ × 58 + ½ × 93 = 75,5 процентах случаев; если вратарь выберет стратегию «справа», ваша стратегия обеспечит вам успех в ½ × 95 + + ½ × 70 = 82,5 процентах случаев. Если вратарь знает, что вы делаете свой выбор по такому принципу, он выберет стратегию «слева», чтобы удержать процент успешных ударов на уровне 75,5 процента. Но это все же больше, чем 70 процентов забитых мячей, которые вы получили бы в случае применения двух чистых стратегий.

Легкий способ проверить, нужна ли такая случайность при выборе стратегий, – попытаться понять, причинит ли вам вред, если вы позволите другому игроку узнать о вашем фактическом выборе до того, как он сделает ответный ход. Если вам это невыгодно, значит случайный выбор, который заставит другого игрока строить догадки, принесет вам пользу.

Можно ли назвать смешивание стратегий по принципу 50:50 лучшим для вас? Нет. Попробуйте другой вариант – когда вы будете выбирать стратегию «слева» в 40 процентах случаев, а стратегию «справа» – в 60 процентах случаев. Положите в карман маленькую книжку, а когда будете готовы подбежать к мячу и сделать удар, достаньте ее и откройте на любой странице (снова так, чтобы не видел вратарь). Если последняя цифра номера страницы попадает в диапазон от 1 до 4, выберите стратегию «слева», а если от 5 до 10 – стратегию «справа». Теперь процент успешных ударов в случае, если вратарь выберет стратегию «слева», составит 0,4 × 58 + 0,6 × 93 = 79, а если стратегию «справа» – 0,4 × 95 + 0,6 × 70 = 80. Вратарь может держать вас на уровне 79 процентов, выбрав стратегию «слева», но это лучше, чем 75,5 процента успешных ударов, которые вы могли бы сделать в случае смешивания стратегий по принципу 50:50.

Обратите внимание на следующий факт: чем лучше пропорции смешивания стратегий игрока, выполняющего штрафной удар, тем меньше разница между показателями успешных ударов в случаях, когда вратарь выбирает стратегию «слева» и стратегию «справа». При выборе чистых стратегий эти показатели составляют 93 и 70 процентов; в случае смешивания стратегий по принципу 50:50–82,5 и 75,5 процента, а при смешивании стратегий в пропорции 40:60–80 и 79 процентов. Очевидно, что смешивание стратегий в оптимальной пропорции обеспечивает один и тот же процент успешных ударов независимо от того, какую стратегию выберет вратарь. Кроме того, это согласуется и с интуитивным предположением, что смешивание ходов – правильный подход, поскольку он не позволяет другому игроку извлекать для себя выгоду из любой системы или закономерности выбора.

Расчеты, о которых пойдет речь в одном из следующих разделов данной главы, свидетельствуют, что для игрока, выполняющего пенальти, лучше всего смешивать стратегии по такому принципу: выбирать стратегию «слева» в 38,3 процентах случаев и стратегию «справа» – в 61,7 процентах. Это обеспечит 0,383 × 58 + 0,617 × 93 = 79,6 процентах забитых мячей, если вратарь выберет стратегию «слева», и 0,383 × 95 + 0,617 × 70 = 79,6 процента забитых мячей, если вратарь выберет стратегию «справа».

А что насчет стратегии вратаря? Если он выберет чистую стратегию «слева», бьющий игрок может получить 93 процента забитых мячей, выбрав стратегию «справа»; если вратарь выберет чистую стратегию «справа», у бьющего игрока есть шансы получить 95 процентов забитых мячей при условии выбора стратегии «слева». Смешав свои стратегии, вратарь может удержать число успешных ударов игрока, выполняющего пенальти, на гораздо более низком уровне. Для вратаря оптимальна та пропорция смешивания стратегий, при которой у бьющего игрока сохранится процент успешных ударов независимо от того, какую стратегию он выберет – «слева» или «справа». С учетом этого условия вратарь должен выбрать смешивание стратегий «слева» и справа» в пропорции 41,7 процента и 58,3 процента соответственно; бьющему игроку это обеспечивает 79,6 процента успешных ударов.

Обратите внимание на следующий факт – на первый взгляд он кажется совпадением: процент положительных исходов, который может обеспечить себе бьющий игрок, выбрав оптимальное смешивание стратегий (а именно 79,6 процента), совпадает с процентом положительных исходов, которым вратарь может ограничить бьющего игрока, выбрав свое оптимальное смешивание стратегий. На самом деле это не совпадение, а важное общее свойство равновесия в смешанных стратегиях в играх с чистым конфликтом (играх с нулевой суммой).

Этот результат, который получил название «теорема о минимаксе», впервые сформулировал математик Принстонского университета, человек энциклопедических знаний Джон фон Нейман. Впоследствии в соавторстве с экономистом Принстонского университета он развил эту идею в классической книге Theory of Games and Economic Behavior [64] , которая и положила начало теории игр.

Теорема о минимаксе гласит, что в играх с нулевой суммой, в которых интересы игроков прямо противоположны (выигрыш одного означает проигрыш другого), один игрок должен стремиться к тому, чтобы минимизировать максимальный выигрыш соперника, тогда как его соперник стремится максимизировать свой минимальный выигрыш. Такой подход к ведению игры приводит к поразительному выводу: минимальный из максимальных выигрышей (минимакс) эквивалентен максимальному из минимальных выигрышей (максимин). Общее доказательство теоремы достаточно сложное, но результат полезен и его стоит запомнить. Если все, что вам нужно знать, – это выигрыш одного игрока или проигрыш другого в случае, когда оба применяют во время игры оптимальное смешивание стратегий, необходимо только рассчитать оптимальную пропорцию смешивания стратегий для одного из них и определить результат такого смешивания.