Сначала рассмотрим алгебраический метод. Число стратегий «слева» в смешанной стратегии игрока, выполняющего пенальти, – это неизвестное, которое нужно найти; назовем его х. Поскольку это относительная доля, число стратегий «справа» составит (1 – х). Показатель эффективности такой смешанной стратегии в случае, если вратарь выберет стратегию «слева», составит 58x + 93(1 – x) = 93–35x процентов, а если он выберет стратегию «справа» – 95x + 70(1 – x) = 70 + 25x процентов. Эти два показателя будут равными, если 93–35x = 70 + 25x, или 23 = 60x, или x = 23∕60 ≈ 0,383.

Мы можем также найти решение графическим методом, отобразив результаты различных вариантов смешивания стратегий на графике. Доля ударов слева в смешанной стратегии бьющего игрока, которую мы обозначили как х, отображается на горизонтальной оси от 0 до 1. По каждому варианту смешивания стратегий одна из двух линий отображает показатель эффективности стратегии бьющего игрока в случае, если вратарь выберет чистую стратегию «слева» (обозначенную на графике буквой Л), а другая – показатель эффективности стратегии бьющего игрока, если он выберет чистую стратегию «справа» (буква П). Первая линия начинается в точке, соответствующей значению 93 (значение выражения 93–35x при х = 0), и опускается до значения 58 (значение этого же выражения при х = 1). Вторая линия начинается в точке, соответствующей значению 70 (значение выражения 70 + 25x при х = 0), и повышается до значения 95 (значение этого же выражения при х = 1).

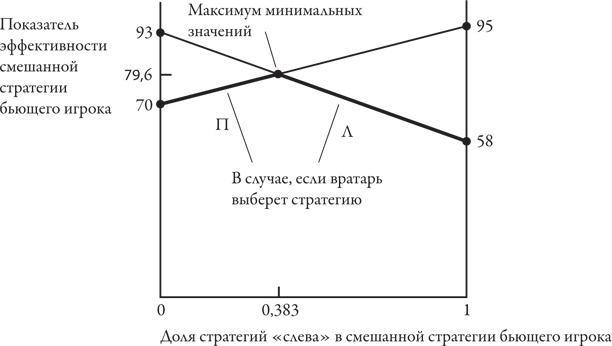
Вратарю необходимо удерживать показатель эффективности стратегии бьющего игрока на как можно более низком уровне. Следовательно, если бы структура смешанной стратегии бьющего игрока была известна вратарю, он выбрал бы стратегию «слева» или «справа», отображенную одним из тех сегментов двух линий, которые расположены ниже точки пересечения. Эти сегменты, выделенные жирным и образующие перевернутую букву V, отображают минимальный показатель эффективности стратегии игрока, выполняющего штрафной удар, если вратарь использует выбор бьющего игрока с наибольшей выгодой для себя. Бьющему игроку необходимо выбрать из этих минимальных значений максимальный показатель эффективности своей смешанной стратегии. Это значение соответствует вершине перевернутой буквы V, то есть точке пересечения двух линий. Внимательно изучив график, получим те же координаты этой точки, которые дает алгебраическое решение: x = 0,383, а показатель эффективности стратегии – 79,6 процента.

Точно так же можно проанализировать смешанную стратегию вратаря. Обозначим число стратегий «слева» в смешанной стратегии вратаря как y. Тогда (1 – y) – это доля стратегий «справа» в его смешанной стратегии. Если бьющий игрок выберет стратегию «слева» против этой смешанной стратегии, средний показатель эффективности его стратегии составит 58y + 95(1 – y) = 95–37y, а если стратегию «справа» – 93y + 70(1 – y) = 70 + 23y. Эти два показателя будут равными, если 95–37y = 70 + 23y, или 25 = 60y, или y = 25∕60 ≈ 0,417.

Графический анализ смешанной стратегии вратаря представляет собой простую модификацию такого же анализа стратегии игрока, выполняющего пенальти. Для этого построим график, отображающий результаты различных вариантов смешивания стратегий вратаря. Доля позиций «слева» в смешанной стратегии вратаря, которую мы обозначили как y, отображается на горизонтальной оси от 0 до 1. Одна из двух линий отображает показатель эффективности стратегии вратаря в случае, если бьющий игрок выберет чистую стратегию «слева», а другая – тот же показатель, если это будет чистая стратегия «справа». По каждому варианту смешивания стратегий, который выберет вратарь, бьющий игрок должен выбрать тот вариант стратегии «слева» или «справа», который обеспечивает более высокий показатель эффективности. Этот максимум находится в вершине буквы V, образованной теми сегментами двух линий, которые выделены жирным. Вратарь должен удерживать показатель эффективности стратегии бьющего игрока на максимально низком уровне. Он может сделать это, выбрав стратегию, соответствующую нижней точке буквы V, то есть минимум максимальных значений. Этой точке соответствуют координаты y = 0,417, а показатель эффективности стратегии – 79,6 процента.

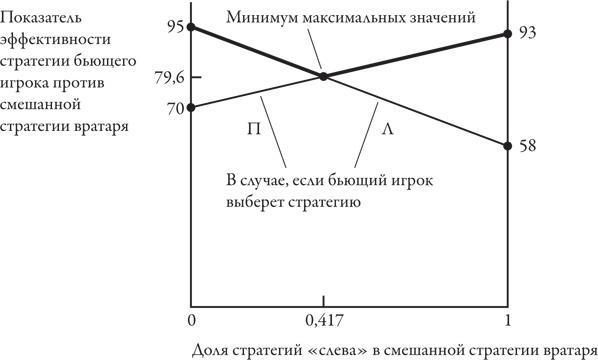
Равенство максимума минимальных значений (максимина) бьющего игрока и минимума максимальных значений (минимакса) вратаря – это и есть теорема фон Неймана – Моргенштерна о минимаксе в действии. Возможно, было бы правильнее назвать ее теоремой о равенстве максимина и минимакса, но общепринятое название короче и легче запоминается.

Неожиданные последствия изменений в смешанных стратегиях

Даже в играх с нулевой суммой равенство смешанных стратегий обладает на первый взгляд необычными свойствами. Вернемся к примеру с футбольным пенальти и предположим, что вратарь усовершенствует навыки отражения штрафных ударов, сделанных с естественной для него стороны (справа), что снизит показатель эффективности бьющего игрока с 70 до 60 процентов. Как это скажется на вероятности смешивания стратегий вратаря в разных пропорциях? Ответ на этот вопрос можно получить, сместив соответствующую линию на графике. Число позиций «слева» в равновесной смешанной стратегии вратаря увеличится с 41,7 до 50 процентов. Это означает, что, если вратарь усовершенствует навыки отражения штрафных ударов справа, он будет реже использовать эту сторону!

Хотя на первый взгляд это кажется странным, причина вполне понятна. Когда вратарь улучшает свою способность отбивать пенальти справа, бьющий игрок начнет реже делать удары справа от вратаря. В ответ на увеличение числа ударов слева вратарь увеличит долю стратегий «слева» в своей смешанной стратегии. Смысл укрепления слабых навыков в том, что вам не придется пользоваться ими так часто.

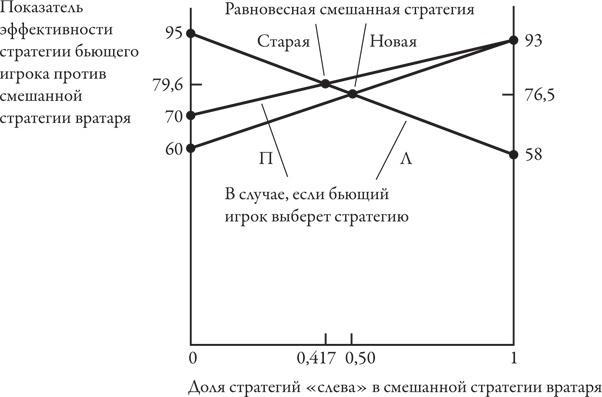
Вы можете проверить истинность этого утверждения, рассчитав долю ударов слева и справа в смешанной стратегии бьющего игрока после такого изменения навыков вратаря. Вы увидите, что доля ударов слева увеличится с 38,3 до 47,1 процента.

Работа вратаря над усилением навыка отражения ударов справа действительно принесет свои плоды: средний процент забитых мячей при равновесной смешанной стратегии снизится с 79,6 до 79,5.

Если хорошо подумать, этот кажущийся парадокс подчиняется обычной логике теории игр. То, что лучше всего для вас, зависит не только от вас самих, но и от действий других игроков. Именно к этому и сводится суть стратегической взаимозависимости.