Так как (1,00333)60 = 1,22, размер месячной выплаты составит 60 х 1,22/0,22 = 333 доллара.

Подведем итоги этой главы упражнениями, которые, надеюсь, поддержат ваш интерес к представленным здесь темам.

УПРАЖНЕНИЯ НА ПРИБЛИЖЕННУЮ ОЦЕНКУ

Решите следующие упражнения на вычисление приближенной оценки; затем сверьте свои ответы и ход вычислений с ответами в конце книги.

УПРАЖНЕНИЕ: ПРИБЛИЖЕННАЯ ОЦЕНКА ПРИ СЛОЖЕНИИ

Округлите эти числа в ту или иную сторону и посмотрите, насколько вы близки к точному ответу.

Устно оцените сумму для следующего столбика чисел, округляя их до ближайших 50 центов.

2,67

1,95

7,25

9,21

0,49

11,21

0,12

6,14

8,31

УПРАЖНЕНИЕ: ПРИБЛИЖЕННАЯ ОЦЕНКА ПРИ ВЫЧИТАНИИ

Оцените ответы следующих задач на вычитание, используя округление до второй или третьей цифры.

УПРАЖНЕНИЕ: ПРИБЛИЖЕННАЯ ОЦЕНКА ПРИ ДЕЛЕНИИ

Скорректируйте числа таким образом, чтобы у вас появилась возможность дать приближенную оценку результатам деления.

УПРАЖНЕНИЕ: ПРИБЛИЖЕННАЯ ОЦЕНКА ПРИ УМНОЖЕНИИ

Скорректируйте числа таким образом, чтобы у вас появилась возможность дать приближенную оценку результатам умножения.

УПРАЖНЕНИЕ: ПРИБЛИЖЕННАЯ ОЦЕНКА КВАДРАТНЫХ КОРНЕЙ

Оцените квадратные корни следующих чисел, используя методы деления и усреднения.

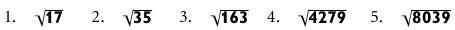
УПРАЖНЕНИЕ: КАЖДОДНЕВНАЯ МАТЕМАТИКА

1. Вычислите 15 % от 88 долларов.

2. Вычислите 15 % от 53 долларов.

3. Вычислите 25 % от 74 долларов.

4. Сколько времени потребуется для удвоения денег при годовой ставке в 10 %?

5. Сколько времени потребуется для удвоения суммы при годовой ставке в 6 %?

6. Сколько времени понадобится для утроения суммы при годовой ставке в 7 %?

7. Сколько времени потребуется для увеличения средств в 4 раза при годовой ставке в 7 %?

8. Оцените размер месячной выплаты за кредит в 100 000 долларов при процентной ставке 9 % в течение 10 лет?

9. Оцените размер месячной выплаты за кредит в 30 000 долларов при процентной ставке 5 % в течение 4 лет?

Глава 6
Математика с ручкой и бумагой

Во введении я упоминал о выгодах, которые вы получите от умения считать в уме. В этой главе я расскажу о том, как ускорить вычисления на бумаге. С тех пор как появились калькуляторы, они успели взять на себя бóльшую часть выполнения арифметических действий во многих ситуациях.

Поэтому в этой главе я предпочел сосредоточиться на забытом искусстве вычисления квадратных корней и методе «крест-накрест» для перемножения больших чисел. Надо сказать, что в основном для разминки мозга, а не для практического применения, я сначала затрону сложение и вычитание и покажу вам парочку любопытных приемов для ускорения этого процесса. Вообще-то эти техники можно успешно использовать в повседневной жизни, в чем вы вскоре убедитесь.

Если вы готовы встретиться с более трудными задачками на умножение, можете пропустить эту главу и сразу перейти к главе 7, критически важной для освоения навыков работы с большими задачами из главы 8. Если же вам нужен перерыв и вы просто хотите немного развлечься, рекомендую прочитать эту главу — вы получите удовольствие от того, что вновь обратились к ручке и бумаге.

СТОЛБИКИ ЧИСЕЛ

Сложение длинных столбиков чисел — как раз та самая задача, с которой вы можете столкнуться по работе или во время подсчета собственных доходов и расходов. Суммируйте числа из следующего столбика привычным способом, а затем посмотрите, как это сделал я.

Когда у меня есть ручка и бумага, я складываю числа сверху вниз и справа налево, как учили в школе. Практикуясь, вы сможете решать эти задачи в уме так же быстро (или быстрее), как и на калькуляторе. Когда я суммирую цифры, единственные числа, которые я «слышу», — это частичные суммы.

Я всегда сначала суммирую крайнюю справа колонку: 8 + 4 + 0 + 7 + 7 + 5 и слышу: 8… 12… 19… 26… 31. Затем я записываю 1, держа в уме 3. Следующая колонка звучит так: 3… 5… 13… 15… 22… 23… 25. Получив итоговый ответ, я записываю его, а затем проверяю свои вычисления путем сложения чисел снизу вверх и обычно получаю такой же результат.

Например, суммирую цифры первой колонки снизу вверх: 5 + 7 + 7 + 0 + 4 + 8 (у меня в голове при этом звучит 5… 12… 19… 23… 31), затем мысленно переношу цифру 3 и складываю 3 + 2 + 1 + 7 + 2 + 8 + 2 и т. д. Благодаря сложению чисел в другом порядке вы снижаете вероятность совершить одинаковую ошибку дважды. Конечно, если ответы отличаются, то хотя бы одно из вычислений было неправильным.

МОДУЛЬНЫЕ СУММЫ

Когда я не уверен в ответе, я проверяю решение, используя метод, который называю «модульные суммы» (потому что он основан на элегантной математике из раздела модульной арифметики [7] ). Он также известен под названиями «цифровые корни» и «метод сравнений по модулю 9». Признаю, что этот метод не слишком практичен, зато он легок в применении.