Магия чисел. Моментальные вычисления в уме и другие математические фокусы | Страница: 39
- Georgia
- Verdana
- Tahoma
- Symbol
- Arial
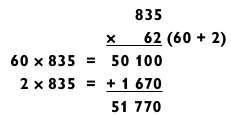
При умножении 6 (из 60) на 5 (из числа 835) появляется дополнительный 0 в ответе, что максимально упрощает задачу на сложение.
Метод вычитания
Как и в задачах на умножение типа «2 на 2», иногда проще решить задачу «3 на 2» путем вычитания вместо сложения, как в следующих примерах.
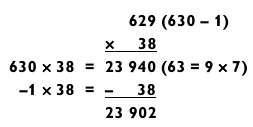
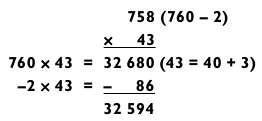
Чтобы сравнить методы вычитания и сложения, применим метод сложения к задаче, которая показана выше.
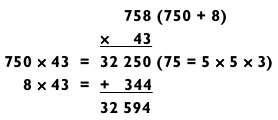
Мое предпочтение при ее решении — использование метода вычитания, потому что я всегда стараюсь оставить максимально легкую задачу на сложение или вычитание на самый конец. В данном случае я бы лучше вычел 86, чем прибавил 344, даже притом, что решить задачу типа «2 на 2» (см. выше) методом вычитания немного сложнее, чем методом сложения.
Метод вычитания тоже можно применять для трехзначных чисел, которые меньше кратного 100 или близки к кратному 1000, как в следующих двух примерах.
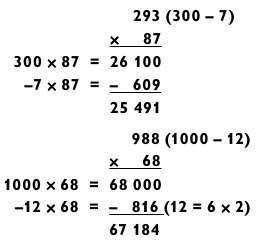
Последние три цифры ответа получены путем использования дополнения для числа 816.
В следующем примере мы умножили на двузначное число с помощью метода вычитания. Обратите внимание, как мы отняли 736 путем вычитания 1000 и обратного прибавления дополнения:
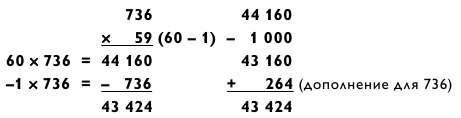
УПРАЖНЕНИЕ: УМНОЖЕНИЕ «3 НА 2»
С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ РАЗЛОЖЕНИЯ, СЛОЖЕНИЯ И ВЫЧИТАНИЯ
Решите представленные ниже задачи типа «3 на 2» с использованием методов разложения, сложения или вычитания.
Разложение, если оно возможно, обычно облегчает задачу. Сверьтесь с ответами в конце книги.

Следующие примеры типа «3 на 2» появятся в разделах по возведению в квадрат пятизначных чисел и умножению типа «5 на 5».

ВОЗВЕДЕНИЕ В КВАДРАТ ПЯТИЗНАЧНЫХ ЧИСЕЛ
Освоение задач на умножение типа «3 на 2» требует значительно больше практики, но как только вы освоитесь с ними, можете сразу переходить к задачам по возведению пятизначных чисел в квадрат, потому что они упрощаются до умножения типа «3 на 2» плюс возведение в квадрат двух- и трехзначных чисел. Например, чтобы возвести в квадрат число 46 792, можно выполнить следующие действия:
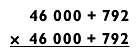
Используя распределительный закон, разделим задачу на такие операции:
46 000 х 46 000 + 2(46 000)(792) + 792 х 792.
Последнее выражение нужно немного упростить:
462 х 1 миллион + (46)(792)(2000) + 7922.
Но я не решаю подобные задачи в последовательном порядке, а начинаю с середины, потому что задача типа «3 на 2» труднее, чем возведение в квадрат двух- и трехзначных чисел.
Итак, в соответствии с принципом «в первую очередь со своего пути убирай сложное», я вычисляю 792 х 46 х 2 и добавляю три нуля в конец результата, то есть выполню следующие действия:
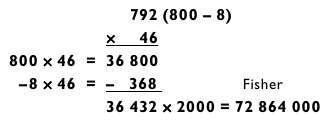
Используя метод вычитания, как показано выше, вычисляем 792 х 46 = 36 432, затем удваиваем результат для получения 72 864. Применение фонетического кода к числу 864 позволяет хранить его в памяти как 72 Fisher.
Следующий шаг: подсчитываем 462 х 1 000 000, что равно 2 116 000 000.
На этом этапе вы можете произнести: «Два миллиарда…».
Активизировав в памяти 72 Fisher, прибавляем к этому числу 116 миллионов, чтобы получить 188 миллионов. Но прежде чем озвучить количество миллионов, нужно проверить, следует ли переносить единицу в старший разряд при сложении Fisher, то есть числа 864 и 7922. Здесь на самом деле не надо вычислять 7922; достаточно определить, что результат вычисления 7922 будет довольно большой, чтобы в сумме с 864 000 превысить 1 миллион. (Вы можете предположить это исходя из того, что 8002 = 640 000, и это число в сумме с 864 000 явно превысит 1 миллион.) Таким образом, к 188 надо прибавить единицу и сказать: «…189 миллионов…».
Все еще держа в памяти слово Fisher, посчитайте квадрат числа 792, используя метод возведения трехзначных чисел в квадрат (округление в большую и меньшую стороны на 8 и т. д.), чтобы получить 627 264. Наконец, прибавьте 627 к Fisher, то есть к числу 864, и получите 1491. Так как мы уже сделали перенос единицы в разряд миллионов, отбросьте первую 1 у числа 1491 и произнесите: «…491 тысяча 264».
Иногда я забываю последние три цифры ответа, поскольку мой мозг полностью поглощен большими вычислениями. Поэтому, перед тем как выполнить итоговое сложение, я сохраняю цифру 2 (из числа 264) на пальцах и стараюсь запомнить 64, что обычно сделать нетрудно, потому что мы имеем склонность к запоминанию того, что слышали недавно. В случае же неудачи я могу восстановить последние две цифры путем возведения в квадрат последних двух цифр исходного числа, то есть 922 = 8464. Последние две цифры этого числа и есть те самые последние две цифры 64. (В качестве альтернативы можно преобразовать число 264 в фонетический код.)