Думай медленно... Решай быстро | Страница: 128
- Georgia
- Verdana
- Tahoma
- Symbol
- Arial
Бернулли предположил, что перспективы оценивают не по ожиданию денежного выигрыша, а по ожидаемой субъективной ценности этого выигрыша. Субъективная ценность игры – снова среднее взвешенное, но теперь отражающее субъективную ценность каждого исхода, взвешенную по ее вероятности. Чтобы объяснить неприятие риска в рамках этого допущения, Бернулли предположил, что субъективная ценность, или полезность, представляет собой вогнутую функцию от денег. В такой функции разница между полезностью, например, 200 долларов и 100 долларов больше, чем разница между 1200 долларами и 1100 долларами. Из вогнутости функции следует, что субъективная ценность выигрыша 800 долларов больше, чем 80% от ценности выигрыша 1000 долларов. Следовательно, вогнутость функции полезности ведет к неприятию риска – выбору гарантированных 800 долларов, а не 80% перспективы выигрыша 1000 долларов, хотя ожидание для обеих перспектив одинаково в денежном выражении.
При анализе решений принято описывать последствия решения в терминах общего богатства. Например, предложение поставить 20 долларов на бросок монеты представляется как выбор между текущим богатством субъекта, W, и равными шансами получить W + 20 долларов или W – 20 долларов. Такое представление выглядит психологически нереальным: люди обычно думают об относительно маленьких деньгах не в терминах изменения богатства, а, скорее, в терминах выигрыша, проигрыша и нейтрального исхода (сохранения статус-кво). Если эффективными носителями субъективной ценности являются изменения богатства, как предлагаем мы, а не итоговое богатство, то психофизический анализ событий должен рассматривать выигрыш и проигрыш, а не общее богатство. Такое предложение играет центральную роль в учении о выборе в условиях, которое мы назвали теорией перспектив (Kahneman and Tversky 1979). Интроспекция и психофизические измерения позволили предположить, что субъективная ценность представляет собой вогнутую функцию от размера выигрыша. Такое же обобщение верно и для проигрышей. Разница в субъективной ценности между потерей 200 долларов или потерей 100 долларов кажется больше, чем разница в субъективной оценке между потерей 1200 долларов или 1100 долларов. Соединив функции ценности для выигрыша и проигрыша, мы получим S-образную функцию, график которой показан на рисунке 1.
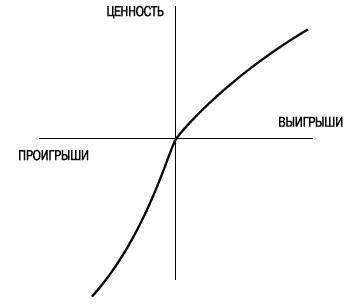
Рис. 1. Гипотетическая функция ценности
Приведенная на рисунке 1 функция ценности (а) определена на выигрышах и проигрышах, а не на полном богатстве, (б) вогнутая на области выигрышей и выпуклая на области проигрышей, (в) значительно круче для проигрышей, чем для выигрышей. Последнее свойство, которое мы назвали «неприятие потерь», выражает догадку, что потеря Х долларов сильнее пугает, чем выигрыш Х долларов привлекает. Неприятие потерь объясняет нежелание людей держать пари с равными ставками: привлекательность возможного выигрыша совершенно недостаточна для компенсации неприятности возможного проигрыша. Например, большинство в выборке студентов отказывались ставить 10 долларов на бросок монеты, если выигрыш составлял меньше 30 долларов.
Допущение о неприятии риска сыграло центральную роль в экономической теории. Однако как вогнутость функции ценности для выигрышей приводит к неприятию риска, так и выпуклость функции для проигрышей приводит к стремлению к риску. В самом деле, стремление к риску в проигрышах – сильный эффект, особенно когда значительна вероятность проигрыша. Рассмотрим, например, ситуацию, в которой человек вынужден выбирать между 85%-ной вероятностью потерять 1000 долларов (и 15%-ной вероятностью не потерять ничего) и гарантированной потерей 800 долларов. Значительное большинство людей предпочитают игру гарантированным потерям. Это выбор стремления к риску, потому что математическое ожидание игры (–850 долларов) ниже ожидания гарантированной потери (–800 долларов). Стремление к риску в области проигрыша было подтверждено несколькими исследователями (Fishburn and Kochenberger 1979; Hershey and Schoemaker 1980; Payne, Laughhunn, and Crum 1980; Slovic, Fischhoff, and Lichtenstein 1982). Это же наблюдалось в отношении событий, не связанных с деньгами, например при выборе продолжительности боли (Eraker and Sox 1981) или приемлемого риска потери человеческих жизней (Fischhoff 1983; Tversky 1977; Tversky and Kahneman 1981). Правильно ли избегать риска в области выигрыша и идти на риск в области проигрыша? Эти предпочтения согласуются с убедительными интуитивными догадками о субъективной ценности выигрыша и проигрыша, и можно предположить, что люди подчиняются своим собственным ценностям. Однако мы еще увидим, что S-образная функция ценности ведет к выводам, нормативно неприемлемым.
Чтобы разобраться с нормативностью, мы обратились к теории принятия решений. Основы современной теории принятия решений содержатся в новаторской работе фон Неймана и Моргенштерна (1974), предложи вшей несколько качественных принципов, или аксиом, которые должны управлять предпочтениями при рациональном принятии решений. В число аксиом входят транзитивность (если А предпочтительнее Б и Б предпочтительнее В, то А предпочтительнее В) и перенос (если А предпочтительнее Б, то равные шансы получить А или В предпочтительнее равных шансов получить Б или В), а также другие, более формальные условия. Нормативный и дескриптивный статус аксиом рационального выбора стал темой широких дискуссий. В частности, существуют убедительные свидетельства, что люди не всегда подчиняются аксиоме переноса, и нормативные достоинства этой аксиомы часто оспариваются (например, Allais and Hagen 1979). Однако любой анализ рационального выбора включает два принципа: доминантность и инвариантность. Доминантность требует следующего: если шанс А (по крайней мере) не хуже шанса Б во всех отношениях и лучше Б хотя бы по одному критерию, то А должно быть предпочтительнее Б. Инвариантность требует, чтобы порядок предпочтения вариантов не зависел от того, в каком виде они представлены. В частности, два варианта, признанные эквивалентными при предложении вместе, должны дать одинаковые предпочтения, будучи предложены порознь. Далее мы покажем, что требование инвариантности, с виду простое и безобидное, обычно не выполняется.
Формулировка исходов путем рамочного анализа (фрейминг)
Перспективы в условиях риска характеризуются возможными исходами и вероятностями этих исходов. Впрочем, одни и те же варианты можно сформулировать или описать по-разному (Tversky and Kahneman 1981). Например, возможные исходы игры можно описать или как выигрыш и проигрыш относительно статус-кво, или как новый размер богатства относительно исходного уровня. Инвариантность требует, чтобы подобные изменения в описании исходов не влияли на порядок предпочтений. Следующая пара задач показывает, как нарушается это требование. Общее количество респондентов в каждой задаче обозначим N; процент выбравших каждый вариант указан в скобках.
Задача 1 (N=152)
Представьте, что в США идет подготовка к эпидемии необычной азиатской болезни, которая, по прогнозам, убьет 600 человек. Предложены две альтернативных программы борьбы с заболеванием. Допустим, точные научные оценки последствий для каждой программы таковы: