Как Мишин отец справился с этой задачей?

99. Почтовые марки

Гражданин купил на 5 рублей марок трех родов: в 50 копеек, в 10 копеек и 1 копейку — всего 100 штук.

Можете ли вы сказать, сколько штук марок разного рода он купил?

100. Сколько монет?

Гражданин получил сдачи 4 рубля 65 копеек рублями, гривенниками и копеечными монетами. Всех монет ему дали 42.

Сколько монет каждого достоинства ему было дано?

Сколько решений имеет эта задача?

101. Почем лимоны?

Три дюжины лимонов стоят столько рублей, сколько дают лимонов на 16 рублей.

Сколько стоит дюжина лимонов?

102. Книжный червь

Есть насекомые, грызущие книги, прогрызающие лист за листом и прокладывающие себе таким образом путь сквозь толщу книги. Один такой «книжный червь» прогрыз себе путь от первой страницы первого тома до последней страницы второго тома, стоявшего рядом с первым, как здесь нарисовано.

В каждом томе по восемьсот страниц.

Сколько всего страниц прогрыз червь?

Задача нетрудная, но не такая уж простая, как вы, вероятно, думаете.

103. Одна лодка на троих

Три любителя речного спорта владеют одной лодкой. Они хотят устроиться так, чтобы каждый владелец мог в любое время пользоваться лодкой, но чтобы никто из посторонних не мог ее похитить. Для этого они держат ее на цепи, которая замыкается тремя замками. Каждый имеет только один ключ, и все-таки он может отомкнуть цепь своим единственным ключом, не дожидаясь прихода товарищей с их ключами.

Как же они устроились, что у них так удачно получается?

104. Из шести спичек

Вот очень старая спичечная задача: из шести спичек составить четыре равносторонних треугольника.

Само собою разумеется, что переламывать спички нельзя.

Задача интересна тем, что с первого взгляда кажется совершенно неразрешимой.

Замысловатые перестановки

Особый вид головоломок — это задачи на перестановки и размещения. У нас приведено несколько таких занимательных задач.

105. Шесть монет

Надо разложить шесть монет в три прямых ряда так, чтобы в каждом ряду было по три монеты.

Вы думаете, это невозможно? Не хватает еще трех монет? А вот поглядите, они расположены на рисунке.

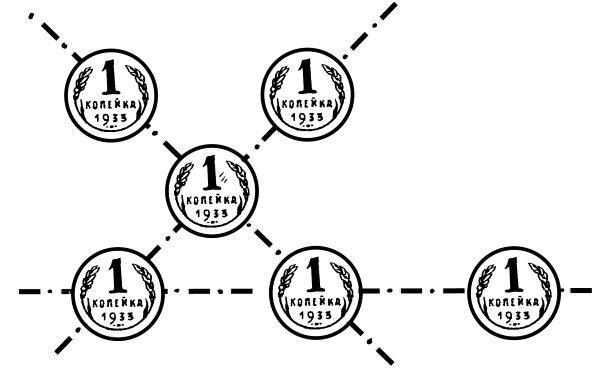
Вы видите здесь три ряда монет по три в каждом ряду. Значит, задача решена. Правда, ряды перекрещиваются, но ведь это не было запрещено.

Теперь попробуйте сами догадаться, как можно решить ту же задачу еще и другим способом.

106. Девять монет

Надо расположить девять монет в десять рядов по три монеты в каждом ряду.

Можно ли это сделать?

107. В пять рядов

Десять монет надо расположить в пять прямых рядов так, чтобы в каждом ряду лежало по четыре монеты.

Прибавлю, что ряды, как и в прежних случаях, могут перекрещиваться.

108. Девять нулей

Девять нулей расставлены так, как здесь показано:

Задача состоит в том, чтобы перечеркнуть все нули, проведя только четыре прямых линии.

Чтобы облегчить отыскание решения, прибавлю еще, что все девять нулей перечеркиваются, при этом не отрывая пера от бумаги.

109. Тридцать шесть нулей

В клетках этой решетки расставлено, код видите, тридцать шесть нулей.

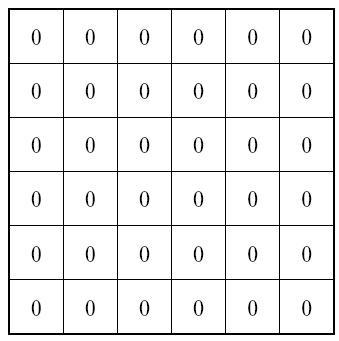
Надо двенадцать нулей зачеркнуть, но так, чтобы после этого в каждом лежачем и стоячем ряду оставалось по одинаковому числу незачеркнутых нулей.

Какие же нули надо зачеркнуть?

110. В девяти клетках

Последняя задача этого отдела шуточная — полузадача-полуфокус.

Составьте из спичек квадрат с девятью клетками и положите в каждую клетку по монете так, чтобы в каждом лежачем и стоячем ряду лежало 6 копеек. Рисунок показывает, как должны быть расположены монеты. На одну монету положите спичку.

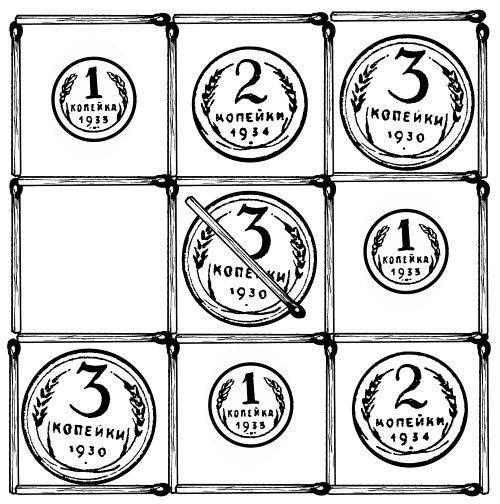
Теперь задайте товарищам задачу: не сдвигая монеты, на которой лежит спичка, изменить расположение монет так, чтобы в лежачих и стоячих рядах было по-прежнему по 6 копеек.

Вам скажут, что это неисполнимо. Однако, при помощи маленькой уловки вы совершаете, это «невозможное» дело. Как именно?

111. Карандаш на острие

Можно ли поставить на палец карандаш так, чтобы он устойчиво держался на своем очинённом конце? «Устойчиво» — значит, так, что, если отвести карандаш в сторону, он не только не опрокинется, но примет снова прежнее положение.

Казалось бы, так удержать карандаш долго на пальце невозможно. Но подумайте, может быть, вы догадаетесь, как это сделать.

112. Монета на пальце

Положите на палец полоску картона такой формы и размера, как железнодорожный билет, а на нее медную монету, например в 5 копеек.

Можно ли теперь удалить картон так, чтобы монета осталась на пальце?

113. Игла на воде

Можно ли положить стальную иглу на воду так, чтобы она не потонула? Многие из вас, наверное, думают, что совершенно невозможно. Однако, если знать, как приняться за дело, то это почти всегда удается сделать.

114. Ходьба и бег

Чем ходьба отличается от бега?