Book.

Конечно, это устрашающее число не оказывало влияния на серьезного аналитика. Большие числа сами по себе не гарантировали безопасности от взлома. Любой человек, решивший криптограмму-головоломку, сумел устранить все кроме одного из 403 291 461 126 605 635 584 000000 различных буквенных замещений. Это было возможно сделать благодаря тому, что буква Е вполне обычна, сочетание АО — редко и т. д. и т. п. Так что каждый мог устранить большое количество вариантов сразу.

Как видно, большое количество коммутационных панелей само по себе не является проблемой. Можно рассмотреть гипотетическую машину, в которой своппинг коммутационной панели применяется только перед зашифровкой с помощью базовой «Энигмы». Предположим, что для такой машины точно известно, что текст F H O P Q B Z является шифровкой слова G E N E R A L.

И опять-таки, имеется возможность ввести буквы F H O P Q B Z в семь соединенных последовательно «Энигм» и проверить, что получается на выходе. Но в этот раз аналитик не ожидает появления букв G E N E R A L, потому что к ним был применен неизвестный своппинг коммутационной панели. Тем не менее, кое-что еще можно сделать. Предположим, что в некоей точке процесса прохода через все позиции ротора сложился такой набор значений:

(26!/ 10!6!2) На самом деле 11 пар дают немного больше способов — правда, тут совсем небольшая разница; 12 или 13 пар иногда меньше, т. е. 26! Это также число возможных подключений проводов к каждому ротору «Энигмы».

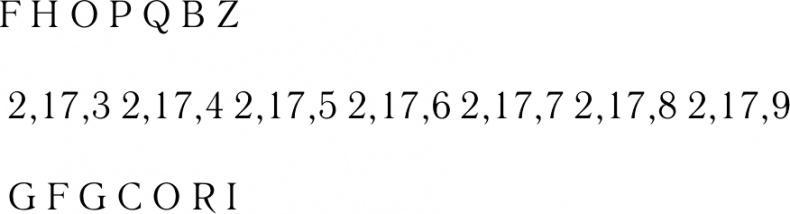
Затем можно задать вопрос: могут ли (или не могут) буквы G F G C O R I быть получены из комбинации G E N E R A L как побочный эффект от своппинга коммутационной панели. В этом примере звучит ответ «нет», потому что при своппинге первая буква G поменяется, а вторая буква G превратится в N, своппинг не может превратить первую букву в слове G E N E R A L в F, а вторую — в C. К этому можно добавить, что своппинг не может превратить букву R в слове G E N E R A L в О, а затем трансформировать А в R. Любого из этих замечаний достаточно, чтобы исключить эту позицию роторов.

Чтобы правильно ответить на вопрос, надо исходить из принципа соответствия. Если загрузить зашифрованный текст в «Энигмы», то будет ли результат на выходе соответствовать известному заранее простому тексту в том плане, что он отличается только в силу своппинга. С этой точки зрения, соответствия (OR) и (RA) или (EF) и (ЕС) являются противоречиями. Но достаточно одного противоречия, чтобы устранить миллиарды возможных коммутационных панелей на этой гипотетической машине. Поэтому огромное число (замещений) может считаться несущественным в сравнении с логическими свойствами шифровальной системы.

Было сделано важнейшее открытие. Его суть заключалась в том, что нечто подобное можно было бы сделать и с реальной военной «Енигмой» со своппингом для коммутационной панели. Ведь он осуществлялся перед и после ввода текста на роторы у базовой «Энигмы». Открытие было сделано далеко не сразу и оно не было плодом раздумий и усилий одного человека. Чтобы сделать этот вывод, ушло несколько месяцев. К его авторам, в первую очередь, следует отнести двух человек. В то время, как Джеффрис присматривал за изготовлением новых перфорированных листов, Алан и Гордон Уэлчмен контролировали разработку изделия, которое позже стало известно как «британская Бомба».

«Атаку» начал Алан, а Уэлчмэн отвечал за анализ потоков информации, поэтому ему первому удалось сформулировать принцип механизации поиска логических соответствий, основанный на «вероятном слове». Польские аналитики механизировали простую форму распознавания, будучи ограниченными используемой тогда системой индикаторов. Новая машина, как ее видел Алан, была намного более амбициозной, требовала наличия проводки для имитации «включений» от гипотетической коммутационной панели и средств распознавания не только простых соответствий, но и появляющихся противоречий.

Теперь предположим, что нам известно, что буквы L A K N Q K R являются шифровкой слова G E N E RA L, и эта шифровка выполнена на «полноценной» «Энигме» с коммутационной панелью. В этот раз нет смысла в проверке сочетания L A K N Q K R на базовых «Энигмах» и в просмотре того, что получается на выходе, потому что перед вводом L A K N Q K R на роторы «Энигмы» к этой комбинации букв был применен неизвестный своппинг коммутационной панели. Но поиски были небесполезны. Рассмотрим только одну букву, а именно А. Существует только 26 вариантов воздействия коммутационной панели на А, поэтому мы можем проверить их все. Начать мы можем с принятия гипотезы (АА), т. е. допустить, что коммутационная панель не повлияла на букву А.

Что следует из этого? Теперь мы можем использовать то обстоятельство, что имеется только одна коммутационная панель, выполняющая одну и ту же своппинговую операцию на буквах, поступающих на роторы и выходящих из них (если бы «Энигма» была оснащена двумя разными коммутационными панелями — одной для своппинга вводимых букв, другой — для своппинга получающихся, то это была бы совсем другая история). Кроме того, мы можем использовать тот факт, что этот конкретный иллюстративный «ключ» содержит одну особенность — замкнутый контур. Проще всего это можно увидеть при выработке возможных обобщений, которые можно сделать из (АА).

Проверяя вторую букву в комбинации, мы вводим А в роторы «Энигмы» и получаем на выходе, например, букву О. Это значит, что коммутационная панель должна содержать своппинг (ЕО).

При проверке четвертой буквы, утверждение (ЕО) будет иметь импликацию для N, например, (NQ); теперь третья буква дает импликацию для К, например (KG).

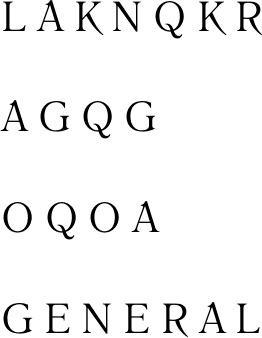
Наконец, мы рассматриваем шестую букву: здесь контур замыкается, и мы получаем либо соответствие, либо противоречие между (KG) и оригинальной гипотезой (АА). Если это противоречие, то гипотеза оказалась ложной и может быть удалена.

Предложенный метод был далек от идеала, потому что полностью зависел от нахождения замкнутых контуров в «ключе». Этот феномен проявлялся не во всех ключах. Но это был метод, который по-настоящему работал, потому что идея с замнутой цепью позволяла перевести работу в электрическую форму. Это доказывало, что огромное количество коммутационных панелей само по себе не являлось непреодолимым препятствием.

Это было начало, и оно стало первым успехом Алана. Подобно большинству научных исследований военного времени, идея не требовала самых совершенных знаний. Скорее здесь была нужна квалификация такого же уровня, что и про проведении перспективных исследований, но применяемая при решении более простых проблем. Идея автоматизации процессов была достаточно известна в двадцатом веке. Ей не был нужен автор «Computable Nambers». Но его серьезный интерес к математическим (вычислительным) машинам, его увлеченность идеей работы машины, были очень важны. Опять же, присущие коммутационной панели условия «соответствия» и «противоречия» касались только сугубо ограниченной проблемы, а не чего-то, подобного теореме Гёделя, которая описывала бесконечное множество теории чисел. Но аналогия с формалистской концепцией математики, в которой импликации должны были механически доведены до логического конца, была поразительна.