Взлом креатива. Как увидеть то, что не видят другие | Страница: 45
- Georgia
- Verdana
- Tahoma
- Symbol
- Arial
Так же ведут себя и люди. Рядом с моим домом есть светофор с дополнительной стрелкой поворота налево. Каждый вечер в левом ряду в ожидании переключения светофора скапливается до 20 машин, а прямо не хочет ехать никто. И каждый вечер я еду прямо, объезжаю квартал и выезжаю на нужную дорогу слева до того, как переключится светофор поворота налево. Как и у того цыпленка, глаза этих водителей зашорены: они могут только стоять в общей очереди, не думая, что повернуть можно через квартал.
Элементарное утверждение «Рассмотрите одну вещь в ее отношении к другой вещи» описывает суть открытия, изобретения, идеи. Открытия и изобретения в каком-то смысле не больше чем рассмотрение двух старых понятий в свете новых отношений. Представьте это в виде математического уравнения с двумя элементами проблемы по каждую сторону относительного слова. Создается элементарное утверждение: «Возьмите одно-другое». Дефис можно заменить одним из 60 основных английских слов, изменяющих взаимоотношения элементов. Вот этот список.
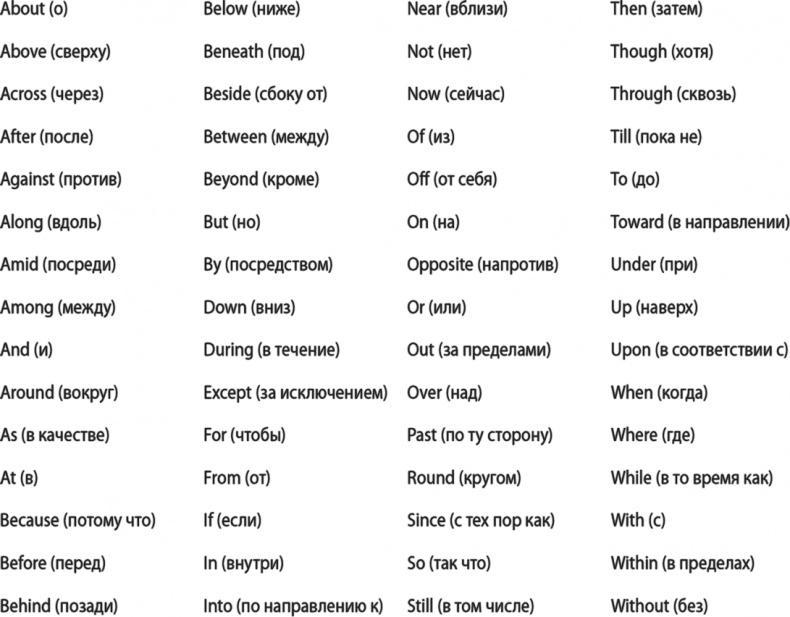
Сценарий
1. Разбейте проблему на ряд элементов.
Пример: команда дизайнеров хотела улучшить холодильник. Среди элементов этой проблемы – «холодильник», «дверь», «морозильная камера», «источник электричества», «отделение для льда», «отделения для продуктов», «внутреннее освещение», «сохранение холодного воздуха», «эстетика» и «цвет».
2. Выберите два основных элемента проблемы.
Пример: «холодильник», «дверь».
3. Выберите относительное слово и вставьте его между двумя элементами проблемы. Успех в решении задачи определяется способностью изменить взаимоотношения между элементами ситуации. Две части концепции проблемы соединяются с помощью одного или нескольких относительных слов, чтобы получились необычные ассоциации. Затем они используются для стимулирования новых идей.
Пример: холодильник без дверей.
4. Изучите это сочетание, записывая все предлагаемые идеи.
Пример: установление отношений такого рода («без дверей») породило изобретение холодильника без дверей. «Торнадо» холодного воздуха циркулирует внутри, а вертикальные потоки создают защитный занавес, не пропускающий теплый воздух. Холодильник круглый в сечении, его можно поставить где угодно, в том числе и в самом центре кухни.
5. Повторите шаги 2 и 3. Продолжайте устанавливать различные типы взаимоотношений, меняя элементы проблемы и относительные слова, стимулируя появление новых идей.
Пример: здесь дизайнеры продолжили поиск дополнительных идей. Перебрав несколько типов взаимоотношений, они остановились на паре «холодильник сбоку от источника электричества», что позволило присоединить к нему небольшую резервную батарею, включающуюся в случае кратковременных перебоев с электроэнергией.
Перебрав возможные типы взаимоотношений и выбрав наилучшее решение, вы можете успешно устранять проблемы. Вот, например, один из парадоксов организации труда: чтобы сотрудники могли творчески реагировать на быстро меняющиеся условия, их надо наделять полномочиями, но в то же время следует сохранять достаточный контроль за действиями по достижению организационных целей. Элементами проблемы в этом случае могут стать «наделение полномочиями», «сотрудники», «организация», «контроль», «цели», «творческая реакция» и «управление». Изучив такой тип отношений, как «наделение полномочиями сотрудников», вы приходите к выводу о необходимости потратить время и энергию, чтобы вызвать в них доверие и привязанность к организации. Создание вовлеченности в работу, доверия и привязанности дает возможность держать компанию под контролем, при этом не контролируя работников, а, напротив, освобождая их.
Стратегия 6
Смотреть на другую сторону
При рассмотрении проблемы мы обычно предполагаем, что существуют определенные границы, в рамках которых и должно лежать решение. Очень часто, однако, оказывается, что границы воображаемые, а решение может находиться и за этими пределами. В 1872 году Рихард Дедекинд первым показал: математики обманывались, считая, что имеют дело с континуумом. По его доказательствам, для чисел континуума не существует. Внутри любого числового предела, например между 1 и 5, есть возможность вставить неограниченное количество чисел. К натуральным числам – 2, 3 и 4 – можно добавить бесконечное количество рациональных дробей типа ¾ или 118/119, а также бесконечное количество чисел иррациональных, например квадратный корень из 2, и место останется в любом случае. Это открытие стало известно как принцип дискретности.
Дискретность быстро стала ключевой темой в модернизме и сформировала новый тип научного, художественного и изобретательского мышления. Физик Людвиг Больцман вскоре продемонстрировал, что непрерывность в физике – такая же статистическая иллюзия, поскольку поведение атомов непредсказуемо. Французский художник Жорж Сёра использовал этот тип мышления, вводя новый метод письма – пуантилизм. Первую современную картину – «Воскресенье после полудня на острове Гранд-Жатт» – он написал тысячами цветных точек, диаметр каждой из которых был не больше трех миллиметров. На этом шедевре изображены около 50 человеческих фигур, собаки и обезьяна, и все это сводится к мелким мазкам краски, которые каким-то образом формируют гармоничное целое, излучающее при этом невероятное спокойствие. Томас Эдисон изобрел кинокамеру, которая тоже стала триумфом дискретности: 16 неподвижных фотографий в секунду наш глаз интерпретирует как движение.
Смена направления
Дедекинд сумел увидеть другую сторону непрерывности, изменив направление своих мыслей о ней. Так родилась блестящая догадка, породившая новый способ мышления в науке и искусстве. Рисунок ниже состоит из неправильных фигур, которые выглядят бессмысленными кусочками пазла. Но если сконцентрироваться на фоне – пространстве между фигурами, – вы заметите слово ЗАПАД. Если вы все еще не видите его, приложите линейку к верхней или нижней границе фигур, тогда оно выступит более явно.

Сосредоточившись на отрицательном пространстве, а не на фигурах, вы изменили угол зрения и увидели то, чего не могли видеть раньше. Вот что бывает, когда меняешь направление обзора и смотришь на другую сторону вещей. Допустим, вам предстоит организовать одиночный теннисный турнир по олимпийской системе. Всего участников 117. Каково минимальное число матчей, которое необходимо организовать для этого количества участников?
Столкнувшись с этой задачей, большинство начнут чертить диаграммы с парами соперников для каждого матча и количеством пустых номеров. Другие попытаются решить задачу математически. Ответ, однако, прост: нужно 116 матчей, и выяснить это просто без всяких сложных расчетов и графиков. Чтобы прийти к нему, смените направление мысли и думайте не о победителях каждого матча, а о проигравших. Поскольку олимпийская система предполагает, что победитель должен быть один, проигравших будет 116. Каждый из них проигрывает лишь единожды, поэтому матчей должно быть 116.