Вместо поэтапного метода вы могли прибегнуть к преобразованию предыдущих решений. Один из весьма интересных способов состоит в использовании решения задачи 4 (см. рис. 17) с модификацией его «методом вычитания». Так как в этой комбинации каждый блок касается пяти других, то идея заключается в уменьшении числа контактов отдельных блоков последовательно, пока оно не составит 1, 2, 3, 4 и 5. Сначала снимем один из верхних блоков и приставим его к одиночному нижнему. Теперь этот нижний блок будет по-прежнему касаться пяти, а остальные – четырех других блоков. Затем снимем один верхний блок и разместим его так, чтобы у блока с пятью контактами их число не изменилось, как и у одного из блоков с четырьмя контактами. Количество контактов оставшегося верхнего блока будет равно трем. Перемещенные вниз блоки имеют один и два контакта соответственно. Задача решена. Окончательная комбинация блоков показана на рис. 21. В ней последний верхний блок слегка повернут. Итак, посредством перемещения всего двух блоков решение задачи 4 превращается в решение задачи 5.

Возможны и другие пути решения этой задачи. Для вас представляет интерес проанализировать выбранный вами метод, насколько он отличается от описанных здесь. Маловероятно, что в данном случае вы нашли лучшие подходы.

Тем из вас, кто не пренебрегает моими комментариями, скажу следующее.

1. Сложные задачи иногда можно решать «по кусочкам». Их условия выполняются последовательно. Этот метод можно назвать поэтапным.

2. Если решение состоит из взаимосвязанных частей, поэтапный метод вам не поможет.

3. При поэтапном методе определяющим является выбор последовательности рассматриваемых стадий. Неверный выбор такой последовательности может завести вас в тупик, верный же не всегда очевиден.

4. Рассмотрение сложной задачи с различных точек зрения иногда способствует ее упрощению.

5. Решение сложной задачи может быть последовательно выведено из решения более простой задачи.

6. Даже если связь новой задачи с предыдущими не очевидна, можно попытаться модифицировать уже известные решения.

7. Модификация «методом вычитания» состоит в последовательном упрощении решения более сложной задачи.

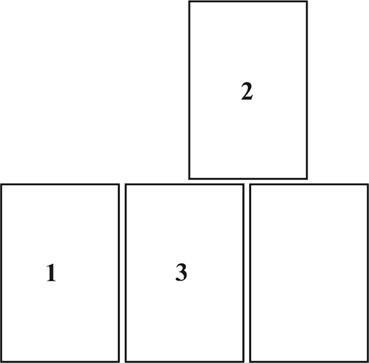
Рис. 18. Комбинация из четырех блоков с одним, двумя и тремя контактами.

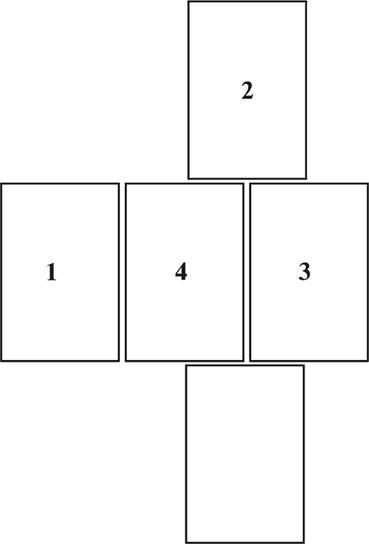
Рис. 19. Комбинация из пяти блоков с одним, двумя, тремя и четырьмя контактами.

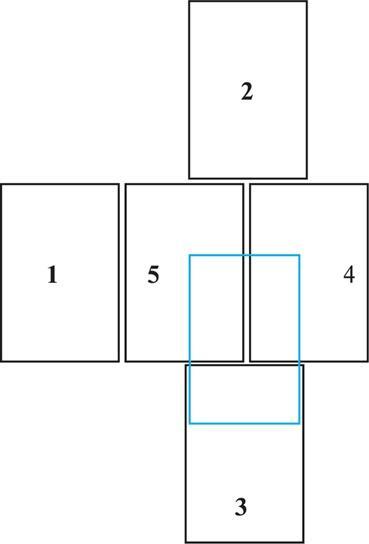
Рис. 20. Решение задачи 5, демонстрирующее число контактов от одного до пяти.

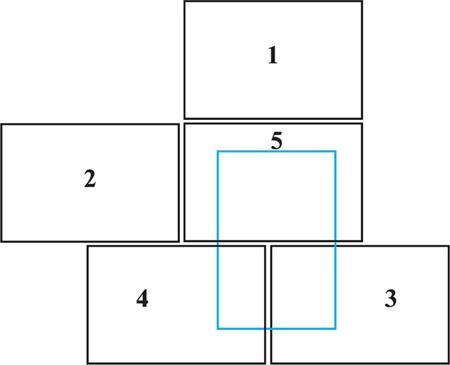
Рис. 21. Решение задачи 5, полученное из решения задачи 4.

Заключение

Обдумывая эти задачи, вы, вероятно, пришли к мнению, что процесс мышления иногда довольно беспорядочен. Возможно, вы предпочли описанные в книге логические подходы или определили их уже после того, как задача была решена. Если ваш подход, хотя и не абсолютно четкий, оказался все же эффективным, вы узнаете намного больше об особенностях своего мышления, нежели человек, облачающий свой случайный успех в мантию логики.

Логический подход обеспечивает, конечно, быстроту и эффективность решения задач (за исключением тех из них, которые требуют генерирования новых идей). К сожалению, практическое мышление далеко уходит от академических рассуждений. Случай, опыт, предрассудки – все оказывает тут влияние. Любопытно, что для решения некоторых проблем при помощи компьютера программы делают лишь частично логичными.

Так как неупорядоченное мышление является скорее приобретенным навыком, не зависящим от математических способностей индивидуума, его можно совершенствовать посредством упражнений и самоанализа (как в задачах этих курсов).

Третий пятидневный курс: L-игра – стратегическое мышление

Введение

Задачи с блоками бьши не так интересны, как с банками. Третий курс связан с игрой, которая может показаться слишком простой. В предыдущих курсах принималось любое пригодное решение. Хотя вас и призывали искать наиболее оригинальное и красивое, это вряд ли оказывало нужное воздействие.

К задачам третьего курса легко найти решение, но здесь необходимо отыскать лучшее из всех возможных. Такие задачи часто возникают в соревнованиях. Новая L-игра является удобной базой для этого курса. Как и ранее, от читателя не требуется ни предварительного опыта, ни специальных знаний.

В отличие от предыдущих задач, игровые ситуации постоянно изменяются, поэтому вашей главной целью становится выработка общих принципов, правил, а не разрешение каждой проблемной ситуации. Это можно назвать стратегическим мышлением.

L-игра

Эту игру придумал автор этой книги, поскольку его увлекают любые игры, хотя он не любит концентрировать свое внимание на большом количестве их элементов. Он хотел сделать игру простой по форме, но объемной по содержанию, требующей нетривиального мышления. Игра должна была удовлетворять следующим условиям:

1) минимальное количество игровых предметов;

2) минимальные размеры игрового поля;

3) минимальное количество правил, простота и доступность;

4) игра должна продолжать быть интересной даже при высочайшем уровне владения ею;

5) игра не должна быть детерминированной. В детерминированной игре типа «крестики – нолики» тот, кто делает первый ход, всегда выигрывает, если знает правильную стратегию. Недетерминированная игра – такая, где два опытных мастера могут «сражаться вечно».

L-игра удовлетворяет всем этим условиям. У каждого игрока имеется по одной L-образной фигуре. Поле состоит из шестнадцати квадратов (4×4). Игра гораздо проще «крестиков – ноликов». Иногда я играл в нее по часу и более. Определенные навыки необходимы, так как есть множество вариантов действий. Поле содержит 18 000 разных позиций для фигур. В игровой ситуации количество возможных ходов может достигать 195.

Правила L-игры

ФИГУРЫ

Каждому игроку дается по одной L-образной фигуре, покрывающей четыре квадрата. Две дополнительные нейтральные фигуры занимают по одному квадрату. Они не принадлежат игрокам, но могут перемещаться любым из них.