Камень ломает ножницы. Как перехитрить кого угодно: практическое руководство | Страница: 25
- Georgia
- Verdana
- Tahoma
- Symbol
- Arial
Полученный при помощи краудсорсинга рейтинг – не эксперимент по имитации случайностей и не исследование первых побуждений. Участников просят выразить отношение к товару цифрой или положением на шкале. Это не так просто, как может показаться. Какой оценки заслуживает данный гастрономический паб, 3 или 4? Должен ли я оценить рекламу кандидата, порочащую соперника, 0 (поскольку я ненавижу негативную рекламу), или 10 (потому что она заставила меня волноваться за соперника)? Рейтинг предполагает выбор цифр, которые соответствуют целой гамме чувств – или полному отсутствию чувств.
Эксперимент Йельского университета можно рассматривать как фокус-группу в поисках товара. Не имея причины давать какую-либо оценку, участники называют первое пришедшее на ум число. Этот элемент присутствует в любом рейтинге, полученном с помощью краундсорсинга. Некоторые либо не имеют никакого мнения, либо думают, что допустим любой ответ. Скорее всего, они выберут нечетную цифру в конце предложенного диапазона, например, 7.
Некоторое время назад было опубликовано исследование, какой смысл подростки вкладывают в слово «нормально». Выбор 7 из 10 подобен угрюмому подростковому «нормально», обычному ответу, который означает «отстаньте от меня». Это одна из причин, почему групповые рейтинги могут быть обманчивыми. Заурядный товар может получить приличную оценку (много семерок), а затем провалиться на рынке. Если вы хотите узнать, купит ли потребитель этот товар, нужно прямо спрашивать его об этом.
В эксперименте в Йельском университете число 0 оказалось самым непопулярным, а за ним следовали 1 и 9 (верхняя граница, поскольку 10 отсутствовало). Это означает, что оценки в районе границ диапазона заслуживают наибольшего доверия. При взгляде на онлайновые результаты обращайте особое внимание на соотношение наименьшей (0 звезд) и наибольшей оценки (5 звезд). Если предположить, что они искренни, то именно этим людям нравится или не нравится продукт.
В отношении многих товаров количество недовольных не имеет значения, пока находится достаточно желающих совершить покупку. Альтернативное кино с высокой долей 5-звездочных оценок, вероятнее всего, понравится тем, кого привлекает имя режиссера или тема, а на количество 0-звездочных оценок можно не обращать внимания. Фильм не предназначен для того, чтобы понравиться кому угодно, и в сети найдется достаточно народу, любящего посмотреть «неправильное» кино. В случае широкой аудитории (например, блокбастера или семейного ресторана) 0-звездочные оценки более информативны. Они позволяют оценить вероятность отрицательного опыта.
Резюме: Как интерпретировать рейтинги, полученные с помощью краудсорсинга
• Люди, которых просят назвать первое пришедшее в голову число в диапазоне от 1 до 10, чаще всего выбирают 7. Это может исказить оценки фокус-групп и рейтинги, полученные в интернете с помощью краудсорсинга.
• Доля участников, присваивающих продукту наивысший рейтинг 10 (или 5 из 5 возможных звезд), может точнее отражать потенциальные продажи продукта, чем усредненная оценка.
11
Как распознать фальшивые числа
Марк Нигрини, выросший в южно-африканском Кейптауне, был очарован магией цифр. Он приехал на учебу в США, надеясь получить докторскую степень в области финансов. В апреле 1989 г. он учился в аспирантуре и подбирал тему для будущей диссертации. Однажды в университете Цинциннати он наткнулся на краткое упоминание закона Бенфорда. «В тот же вечер я отправился в библиотеку и взял статью Бенфорда», – вспоминал Нигрини. Знакомство с ней изменило всю его жизнь.
Физик Фрэнк Бенфорд в 1920-х гг. работал в компании General Electric в городе Скенектади. В то время для научных расчетов использовались таблицы логарифмов. Бенфорд заметил: первые страницы книжки с таблицами логарифмов истрепались от многократного использования, а последние выглядели почти новыми. Именно это случайное наблюдение, а не работа, за которую ему платила General Electric, послужило причиной того, что имя Бенфорда осталось в истории.
Числа, которые требовались Бенфорду, обычно начинались с маленьких величин, а именно они находятся в начале логарифмических таблиц. Так, например, Бенфорд обнаружил, что около 30 процентов чисел, с которыми имеют дело ученые и инженеры, начинаются с цифры 1. И только 5 процентов – с цифры 9. Поэтому последние страницы книги с таблицами логарифмов оставались практически нетронутыми.
Бенфорд рассказал об открытии химику Ирвингу Ленгмюру (будущему лауреату Нобелевской премии). Ленгмюр убедил его опубликовать статью на эту тему. Отличавшийся методичностью Бенфорд исследовал непонятную закономерность еще десять лет. Выяснилось, что она справедлива не только для научных расчетов. Бенфорд попытался проанализировать первые цифры бейсбольной статистики и обнаружил такое же распределение. Он выписал все числа, встречавшиеся в журнале Reader’s Digest. То же самое. Счет теннисных матчей, котировки на бирже, длина рек, атомные веса, счета за электричество на Соломоновых островах и числа, встречающиеся на первой странице New York Times – все подчинялось одной и той же закономерности. Похоже на теорию заговора. Все взаимосвязано.
Наконец, в 1938 г. Бенфорд опубликовал результаты в журнале Proceedings of the American Philosophical Society. В статье он привел точную формулу для вычисления пропорции чисел, начинающихся с каждой цифры. Вот они:
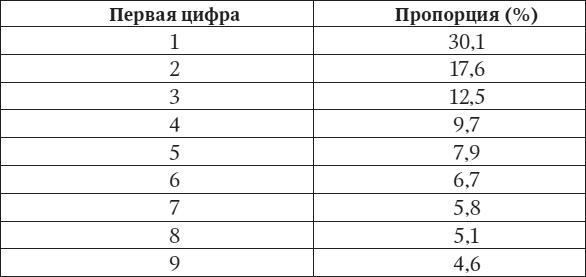
Вы можете спросить, почему здесь отсутствует цифра 0. Бенфорд анализировал только первые ненулевые цифры. Поэтому числа 7129600 и 0,000072002 начинаются с одной и той же цифры 7.
Формула Бенфорда также предсказывает распределение вторых, третьих и так далее цифр числа. В этих случаях уже присутствует 0. Однако преобладание низких величин здесь уже менее выражено. По этой причине выявленную Бенфордом закономерность иногда называют законом первой цифры.
Сам Бенфорд выбрал для статьи другое название, «Закон аномальных чисел» (The Law of Anomalous Numbers). В настоящее время он известен как закон Бенфорда. Как выяснилось, это несправедливо. Данное явление обнаружил (и опубликовал статью) другой, гораздо более известный ученый – астроном Саймон Ньюком. Его статья в номере журнала American Journal of Mathematics за 1881 г. начиналась с констатации факта: «То, что десять цифр встречаются с разной частотой, должно быть очевидно всякому, кто часто пользуется логарифмическими таблицами и замечает, насколько первые страницы истрепаны сильнее последних».
Мне кажется, это очередное доказательство того, как трудно придумать что-то свое и как часто остаются незамеченными даже оригинальные идеи. По какой-то причине о статье Ньюкома вскоре забыли, а статья Бенфорда получила поддержку. Одно из возможных объяснений в том, что статья Бенфорда «выехала» на знаменитой статье физика Ханса Бете, которая была помещена в журнале сразу же вслед за ней.