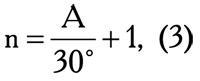
затем, подставляя в формулу (2) найденное значение n, получается В.

Например, 23° Весов требуется перевести в абсолютную величину.

В этом случае А = (7−1) × 30° + 23° = 180° + 23° = 203° Чтобы 255° перевести в относительную величину, необходимо сначала найти номер знака: n = 255°: 30° + 1 = 8 + 1 = 9. Тогда В = 255° − (9−1) × 30° = 255° − 240° = 15°.

Поскольку девятым знаком Зодиака является Стрелец, искомое значение относительной величины будет 15° Стрельца.

При относительно небольшой практике подобные вычисления легко делаются в уме.

Для анализа какой-либо карты координаты лучше выражать в относительных величинах, а для больших расчетов, особенно при вычислении аспектов, лучше пользоваться абсолютными координатами.

Виды эфемерид планет

Эфемеридами называются таблицы, в которых представлены расчеты координат небесных объектов (планет, планетных узлов, неподвижных звезд, фиктивных точек и т.д.). Обычно эти расчеты приводятся на начало каждых суток, однако в принципе периодичность может быть любая.

Существуют различные таблицы эфемерид, из которых следует отметить как наиболее употребительные американские таблицы эфемерид Майкельсона [49, 50, 82, 83] и английские эфемериды Рафаэля [85].

Лучше всего использовать американские эфемериды на полночь, рассчитанные на 100 лет.

Рафаэлевские эфемериды в Англии на полдень выпускаются ежегодно. Они удобны для текущих расчетов транзитных ситуаций, для хорарных карт, так как занимают малый объем, их можно носить в папке или портфеле, даже в широком кармане. В них много полезных дополнительных сведений, например аспектарий. Однако для расчета карт в большом диапазоне временных значений они неудобны.

Эти два вида изданий содержат эфемериды, то есть положения (эклиптические координаты) планет в знаках Зодиака на каждый день. Только американские эфемериды рассчитаны на полночь по Гринвичу, а английские – на полдень. Этого не следует забывать, чтобы не ошибиться в расчетах.

Есть и другие эфемериды. Например, в Немецком астрологическом ежегоднике [81] эфемериды планет даются на каждые 10 дней. Эти таблицы занимают мало места, но менее удобны с точки зрения точности расчетов и годятся лишь для приблизительных вычислений.

Очень любопытны эфемериды, составленные студентом Политехнической школы в России еще в начале прошлого века [71]. Книга объемом менее 100 страниц позволяет рассчитывать эфемериды планет, за исключением Плутона, на 4000-летний период (с 1000 г. до н.э. по 3000 г. н. э.). Однако неудобство этих эфемерид заключается в том, что окончательные расчеты ведутся путем геометрических манипуляций с круговыми номограммами, используя промежуточные данные, полученные в результате сложения трех чисел из трех отдельных таблиц. Следовательно, вычисления громоздки и требуют много времени. Второй основной недостаток этих эфемерид – неточность результатов вычислений. Однако они незаменимы, когда речь идет о приближенных вычислениях для отдаленных периодов (здесь речь идет о ручных расчетах).

Есть еще одна книга таблиц эфемерид для периода с 2500 г. до н.э. по 2000 г. н. э. [90]. Там даются эфемериды на каждые 10 дней, но только для 5 планет, исключая Солнце, Луну и высшие планеты.

Расчет эфемерид планет

Большинство таблиц эфемерид дают положение планет на начало каждого дня. Однако часто необходимо знать положения планет и других небесных объектов в любой момент времени в течение дня с точностью до угловых минут, а в некоторых случаях даже до угловых секунд.

Для точных расчетов вручную существуют формулы линейной интерполяции.

На рис. 34 представлено линейное изменение функции Y в зависимости от аргумента Х, где Xa и Xb – время для начала и конца суток; Х – время, для которого ведется расчет координат планет; Ya и Yb – координаты планет на начало и конец суток; Y – координата планеты на требуемое время Х.

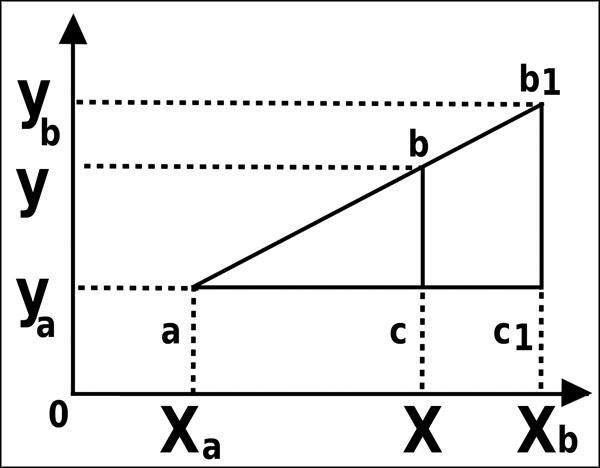
Рис. 34. Геометрическое изображение линейной функции для расчета координат планет

Составив пропорцию на основе подобия получившихся треугольников abc и ab1c1, получим уравнение:

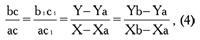
откуда искомое

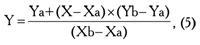
Произведем упрощения: Xb − Xa = 1 суткам или 24 часам из условия, что Xa = 0; X − Va = X – величина постоянная для всех планет. Назовем ее К.

Тогда базовая формула для расчета координат планет такова:

Y = Ya + (Yb – Ya) × K, (6)

Поскольку в таблицах время дается по Гринвичу, К – это GT на искомый момент, выраженное в сутках. Если GT выражено в часах, то:

К=GT / 24, (7)

если в минутах, то:

К = GT / 1440, (8)

Итак, первый этап расчетов – вычисление значения К, равного GT. Как определять GT, уже известно из раздела «Небесная динамика», где шел разговор о системе времен. Вновь приведем формулы расчета в зависимости от гражданского времени Т, принятого в данном регионе в данный период:

GT = Tп − N, (9)

GT = Tд − (N + 1), (10)

GT = Tл − (N + 2), (11)

где GT – среднее солнечное время на Гринвичском меридиане;

Тп – поясное время;

Тд – декретное время;

Тл – летнее время.

Гражданское время обычно называют местным. Не следует это понятие путать с местным временем, известным из раздела «Небесная механика», которое определяется из условия, что в полдень в данном конкретном месте Солнце должно находиться в верхней кульминации.

В справочнике, составленном И.К. Бариевым и С.В. Ликановым [9], приводятся сведения о том, когда в России (точнее, в бывшем СССР) производились ввод и отмена декретного и летнего времени. Следует добавить, что с 1999 года. в России летнее время стали отменять не в сентябре, а в последнее воскресенье октября в 2 часа ночи, как это делается в Европе. А с осени 2011-го перестали переводить два раза в год стрелки часов, оставив летнее время.

На втором этапе вычисляются координаты планет по формуле (6) и заносятся в табл. 19.

Определив координаты планет, переходят к расчету аспектов между ними. Для этого переводят относительные координаты планет в абсолютные, для учебных целей можно округлить значения координат планет до целых значений. Вот только для более точного расчета аспектов надо округлять, если меньше полградуса, то до меньшего целого значения, если больше полградуса, то до большего. Однако в этом случае есть риск ошибиться в численном значении, когда будут использоваться сабианские градусы [68], ибо, как мы условились, в соответствии с требованиями, приведенными Дейном Редиером [68], считать градусы от 1 до 30. В этом смысле и 0° 01′ и 0° 59′ будут считаться первым градусом, а 29° 01′ и 29° 59′ – 30-м градусом. Поскольку в данном курсе заниматься сабианскими градусами не предусмотрено, то можно округлять полученные числа по обычному правилу, о котором говорилось выше.