Что такое ДЭРА?

Остеопороз не поражает все кости равномерно, и одни из них могут оказаться слабее других. Однако сам процесс носит системный характер и затрагивает все кости. Современная медицина определяет остеопороз как значительное отклонение параметров от нормы, установленное в результате специфического обследования – ДЭРА. Минеральная плотность костной ткани измеряется путем определения количества поглощенной энергии при прохождении рентгеновского пучка через ту или иную кость. Оно пропорционально количеству кальция и других минералов в данном участке кости: чем больше минералов, тем меньше энергии поглощается костной тканью. В большинстве случаев обследуются тела поясничных позвонков, подвздошная и бедренная кости, так как именно в этих местах чаще всего происходят переломы.

Результаты ДЭРА указывают на то, какой объем минералов находится между устройством, посылающим рентгеновский пучок, и детектором. На результат влияют два фактора: плотность кости и ее физические параметры. У тонкой, но более плотной ткани показатель минеральной плотности может оказаться таким же, как у более толстой, но более рыхлой кости. Этот показатель отражает лишь количество минерала в ткани, через которую прошел рентгеновский пучок.

Конечно, минеральная плотность костной ткани не единственный фактор, от которого зависит вероятность перелома. Важны также длина костей, прочность связок, количество костных перекладин, координация движений, психическое состояние человека и качество поверхностей, по которым он привык ходить. Но, несмотря на отсутствие знаний о внутреннем строении кости и даже не учитывая личные факторы и факторы окружающей среды, мы знаем, что чем ниже минеральная плотность костной ткани по результатам ДЭРА, тем выше риск перелома. В одногодичном исследовании с участием 197 848 американок постклимактерического возраста, представляющих пять различных этнических групп, снижение МПКТ на одно стандартное отклонение сочеталось с 50-процентным повышением риска перелома в каждой этнической группе. Что такое стандартное отклонение?

Чтобы правильно прочитать результаты ДЭРА, нужно знать статистику. Ваши показатели будут сравниваться с показателями других людей, в частности со средними показателями пиковой прочности костей и с результатами тех, кто схож с вами по возрасту и росту.

Стандартным отклонением, обозначаемым греческой буквой «сигма» (σ), является численный показатель того, насколько тесно сгруппированы члены того или иного множества. По нему можно определить степень удаленности отдельных единиц множества от среднего значения. Математическая формула позволяет рассчитать точное отклонение разных частей группы от среднего показателя. При нормальном распределении 68,2 процента группы всегда будут находиться в пределах одного стандартного отклонения выше или ниже середины. При большой величине стандартного отклонения 68,2 процента группы все равно будут в одном стандартном отклонении от среднего показателя, но расстояние между ее показателем и средним будет больше, поскольку стандартное отклонение больше. В любом случае существует среднее значение, но при большем стандартном отклонении многие люди будут достаточно существенно отличаться от этого значения. Меньшее стандартное отклонение указывает на то, что большая часть группы близка к среднему показателю.

Стандартное отклонение варьируется в зависимости от расхождения между средним значением и различными индивидуальными значениями, но всегда включает в себя 68,2 процента результатов. Два стандартных отклонения будут включать в себя 95 процентов результатов. И лишь 1 процент членов группы будет находиться далее двух с половиной стандартных отклонений от среднего значения.

Пользуясь такой системой расчета, ученые могут определить, насколько значимо отличается некий конкретный показатель от среднего и каковы шансы, что этот показатель означает действительно аномальное состояние, а не случайный вариант нормы.

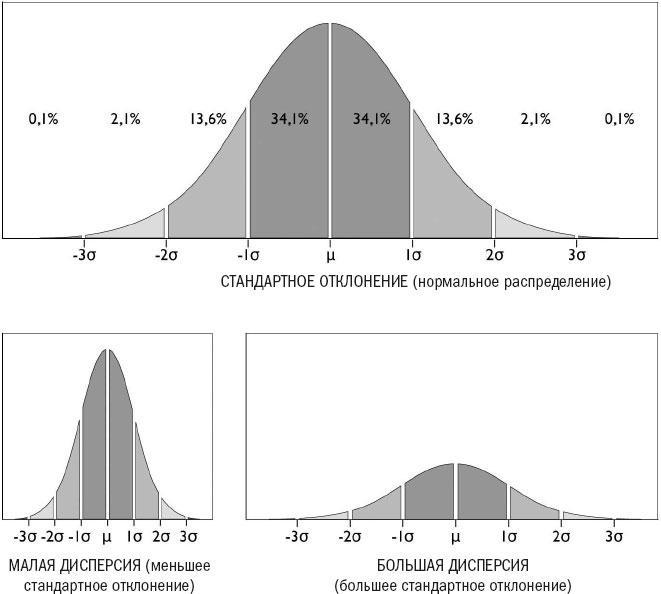
Рисунок 2. В каждом случае стандартное отклонение (σ) означает удаленность от среднего показателя (μ) и включает в себя 68,2 процента результатов.

Пример: стандартные отклонения на практике

Предположим, что группа детей не нашла лучшего занятия, чем пострелять из лука, пытаясь попасть в яблочко большой, умеренно удаленной мишени. Предположим также, что к вечеру в мишени оказалась тысяча стрел, каким-то образом рассредоточенных по всей поверхности. На рисунке 3 изображены два возможных варианта расположения стрел.

Захотев узнать, как близко в среднем к яблочку попали стрелы, мы могли бы измерить расстояние от каждой стрелы до центра мишени, суммировать эти расстояния и разделить сумму на общее количество стрел. Допустим, одна стрела на рисунке 3А оказалась в 4 футах от яблочка, другая – в 14 футах, третья – в 9 футах, четвертая – в 23 футах и так далее. Если сложить расстояния тысячи стрел, получится 10 000. Таким образом, среднее расстояние стрел до центра мишени составит 10 футов. Расчет стандартного отклонения показывает, насколько разнообразны положения разных стрел с учетом их отдаленности от среднего показателя в 10 футов.

Статистики используют формулу, по которой расстояние каждой стрелы до яблочка вычитается из 10 и результат возводится в квадрат. Чем больше итоговое число, тем выше стандартное отклонение. Как видим, на данном рисунке положения стрел значительно отличаются друг от друга, поэтому число будет большим.

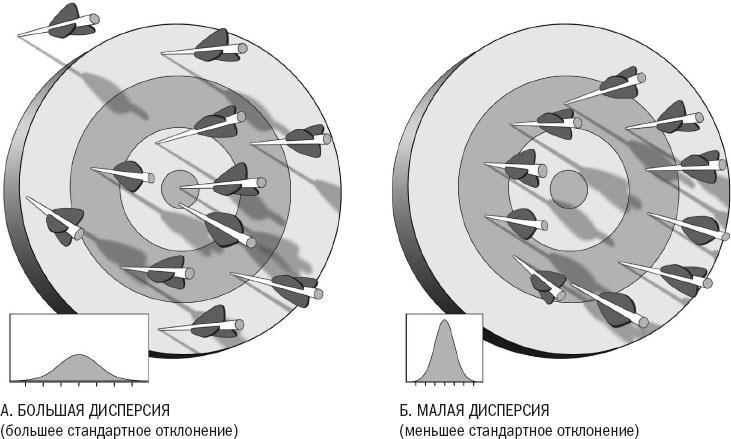
Рисунок 3. Несмотря на то что обе группы стрел имеют одинаковое среднее расстояние до яблочка, величина стандартного отклонения в них разная.

Теперь рассмотрим второй вариант, рисунок 3Б, и рассчитаем стандартное отклонение. В среднем расстояние от стрелы до центра мишени снова составляет 10 футов. Но стандартное отклонение, определенное путем вычитания расстояния каждой стрелы из среднего показателя, будет весьма небольшим. Это небольшое число говорит о том, что положения отдельных стрел относительно яблочка практически одинаковы.

На первой картинке стрела, удаленная на 20 футов от центра мишени, не имеет существенного значения. Хотя это расстояние в два раза больше среднего, оно в данном случае не редкость. По-другому можно сказать, что стандартное отклонение очень большое. Следовательно, стрела, оказавшаяся в 20 футах от яблочка, находится менее чем в одном стандартном отклонении от среднего показателя и может считаться довольно вероятным явлением.

Нас повсюду окружают какие-то группы похожих явлений – от размера отпечатков человеческих ног на пляже до результатов общенационального тестирования. Очень плотная сгруппированность показателей заслуживает пристального внимания и заставляет нас задаться вопросом: «Почему стрелы выстроились на мишени так, как показано на рисунке 3Б?» Может быть, завихрения воздуха или магнитная воронка увлекли за собой наконечники всех стрел и выстроили их на мишени плотным кольцом? Причина неизвестна, но сила статистики такова, что мы можем обойтись и без этого знания. Учитывая стандартное отклонение в случае, изображенном на рисунке 3Б, стрела, угодившая в мишень в 20 футах от центра, была бы большой редкостью. Она оказалась бы во множестве стандартных отклонений от среднего значения. Ее положение потребовало бы объяснений.