Book.

Как и в европейских школах до недавнего времени, образование часто находилось в руках духовенства. Частные школы открывались в домах храмовых служащих, вроде Ур-Уту – жреца kalamahhum в городе под названием Сиппар-Амнанум, находившемся в 80 км от Вавилона. В его доме обнаружили несколько тысяч табличек с написанными учениками упражнениями. Но огромная разница между религией Месопотамии и христианством выражается в явном отсутствии точно определенного религиозного обучения. Нет текстов, в которых обсуждается божественная природа; нет табличек с рассуждениями о смысле жизни; нет документов, излагающих богословское учение или предписания, как правильно поклоняться богам. И хотя многие религиозные мифы и гимны многократно писались и переписывались в качестве письменных упражнений, образование, которое получали ученики, по-видимому, было в основном светским, что представляет собой огромный контраст по сравнению с современной системой образования, которой потребовалось почти 2 тысячи лет, чтобы дистанцироваться от церкви – своего изначального спонсора.

Так как школьное обучение в Вавилоне ограничивала элита – ей суждено было заполнять все вакансии, для которых требовалась грамотность, – ученики получали общее образование на основе учебного плана, не имевшего ничего общего с узким профессиональным обучением. У будущих писцов, обучавшихся не только всему тому, что им будет необходимо в профессиональном плане, было свободное расписание, которое включало все знания того времени. Без сомнения, каждый из них получал дальнейшее образование при вступлении в свою взрослую профессию, какой бы она ни была. Счетовод, администратор, архитектор, астролог, клерк, переписчик, военный инженер, нотариус, священник, писец, изготовитель печатей, секретарь, землемер, учитель – вот лишь некоторые профессии, которые нам известны. Но основы дальнейшего учения закладывались в школах.

Из недавнего резюме выпускника явствует, что арифметика считалась не менее важной для образования в Вавилонии, чем чтение и письмо. Более внимательный взгляд на то, как искусство работы с цифрами преподавали и изучали, рассказывает нам многое о том, каким являлся подход в Вавилонии ко всем формам знаний.

Для начала мы должны признать, что способность манипулировать цифрами была более развита в те древние времена, чем в эпоху европейской истории. В своей книге «За пределами способности к количественному мышлению» математик Джон Аллен Паулос рассказывает анекдот о средневековом немецком торговце, который спросил, куда ему следует отправить учиться своего сына, чтобы тот получил математическое образование. «Если вы хотите, чтобы он овладел сложением и вычитанием, – был ответ, – подойдет местный университет. Но если вы хотите, чтобы он также умел выполнять умножение и деление, вам придется отправить его учиться в Италию». Такие ограничения не относились к вавилонским школам. Но у них было преимущество. Их способ написания чисел намного превосходил римские цифры, которыми европейцам приходилось пользоваться до начала нашего времени. Здесь была самая древняя известная форма «позиционной нотации» – сотни, десятки и единицы, которые мы узнаем в детстве. Эта система отличалась от нашей современной лишь тем, что, используя так называемые арабские цифры, мы делаем каждую позицию слева в 10 раз больше, в то время как вавилоняне – в 60 раз. То, что они писали как (ТТТТ(ии)), нашими цифрами означало 216 000 + 3600 + 60 + 1, то есть 219 661. Как хорошо известно, мы по-прежнему сохраняем вавилонскую систему чисел, основанную на числах кратных 60, когда мы говорим, что 95 652 секунды – это 26 часов, 34 минуты и 12 секунд, или когда мы пишем величину угла как 26°34′12″. Для вавилонян это число выглядело так: .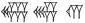

Двумя символами, которых у вавилонян не существовало, были ноль и десятичная запятая. Имея возможность вместо ноля оставлять пробел в числе, как правило, они этого не делали. В результате только по контексту можно было отличить 26, 206, 2006, 260 или 2600. Пройдет еще не одна тысяча лет, прежде чем арабы распространят у себя взятое у индийцев понятие о том, что пустое место в ряду цифр можно обозначить, как и любое другое число (для его обозначения арабы использовали точку; наш ноль на самом деле пришел к нам из книги раввина Авраама ибн Эзры Sefer ha-Mispar – «Книги чисел», которая дала самое первое объяснение индо-арабских чисел; она была написана на древнееврейском языке и опубликована в Европе в Вероне в 1146 г.). На самом деле жители Месопотамии в конечном счете придумали способ обозначения пробела в числе, но гораздо позже, возможно не раньше 700 г. до н. э. И не для того, чтобы его использовать в конце числа. Числа в Вавилонии всегда были верны «плавающей десятичной запятой»: 26, 260, 2600, равно как и 2,6; 0,26 и 0,026 всегда изображались одинаково.

Производить действия в системе счисления, основанной на 60, а не 10, как у нас сегодня, оказывалось камнем преткновения для школьников, пытавшихся запомнить таблицу умножения. До десяти легко выучить наизусть, можно и чуть дальше. До перехода на десятичную систему исчисления британской денежной системы ученикам приходилось волей-неволей запоминать таблицы умножения до двенадцати, так как в шиллинге было 12 пенсов. Дюжины также по-прежнему оставались в широком ходу, и каждый школьник знал, что дюжина дюжин – это гросс. В начале компьютерной эры было полезно писать числа кратные 16, известные как шестнадцатеричная система счисления; приходилось вводить шесть дополнительных цифровых знаков: за цифрами от 1 до 9 следовали буквы от А до F. Многие компьютерные энтузиасты знали наизусть таблицы умножения до 16. Но держать в голове таблицы умножения для каждого числа до 60 – это уж слишком. Так что, проходя мимо вавилонской школы, мы, вероятно, не услышали бы знакомый хор детских голосов: «Дважды один – два, дважды два – четыре». А если бы и услышали, то уж точно не «тридцать один умножить на пятьдесят три – тысяча шестьсот сорок три». Вместо этого вавилонянам приходилось прибегать к таблицам умножения, написанным на глиняных табличках.

Использование таких таблиц, чтобы выполнить умножение даже очень больших чисел, было относительно простым, однако деление представляло собой проблему. Вавилоняне решали ее способом аналогичным тому, который признают большинство людей, которые ходили в школу до последней трети XX в. В тех случаях, когда мы сверялись с таблицами десятичных логарифмов, что давало возможность выполнять большие вычисления с применением только сложения и вычитания, они использовали таблицы обратных величин: единица, поделенная на соответствующее число (например, величина обратная двум – это одна вторая, или 0,5, обратная четырем – одна четвертая, или 0,25, обратная пяти – одна пятая, или 0,2). С таблицами обратных величин под рукой они могли превращать деление в умножение, потому что деление на какое-то число – это то же самое, что умножение на обратную ему величину: 12 разделить на 4 – это то же самое, что 12 умножить на 0,25.

Часто использовали и другие таблицы – квадратов и кубов, равно как и корней квадратных и кубических. С ними вавилонские ученики справлялись с по-настоящему сложными математическими задачами. Они умели решать линейные уравнения – метод, схожий, как отмечают современные математики, с методом исключения Гаусса – квадратные и кубические уравнения, вычислять гипотенузу прямоугольного треугольника (теорема Пифагора) и площадь многоугольников, работать с окружностями и хордами окружностей – они называли их тетивой. Вычисленное ими приближенное значение пи составляло 31/8 или 3,125, что не сильно отличается от величины, которую используем мы, – 3,14159; по крайней мере, она ближе, чем значение 3, установленное в Библии приблизительно тысячелетием позднее.